Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T16:58:43.875Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIMITIVE SUBGROUPS AND PST-GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  18 July 2013

A. BALLESTER-BOLINCHES ,
J. C. BEIDLEMAN  and
R. ESTEBAN-ROMERO
A. BALLESTER-BOLINCHES
Affiliation:
Departament d’Àlgebra, Universitat de València, Dr. Moliner 50, 46100 Burjassot, València, Spain email [email protected]@uv.es
J. C. BEIDLEMAN*
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY 40506-0027, USA
R. ESTEBAN-ROMERO
Affiliation:
Departament d’Àlgebra, Universitat de València, Dr. Moliner 50, 46100 Burjassot, València, Spain email [email protected]@uv.es
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All groups considered in this paper are finite. A subgroup 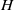$H$ of a group 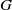$G$ is called a primitive subgroup if it is a proper subgroup in the intersection of all subgroups of 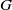$G$ containing 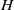$H$ as a proper subgroup. He et al. [‘A note on primitive subgroups of finite groups’, Commun. Korean Math. Soc. 28(1) (2013), 55–62] proved that every primitive subgroup of 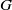$G$ has index a power of a prime if and only if 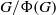$G/ \Phi (G)$ is a solvable PST-group. Let 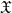$\mathfrak{X}$ denote the class of groups 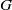$G$ all of whose primitive subgroups have prime power index. It is established here that a group 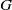$G$ is a solvable PST-group if and only if every subgroup of 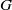$G$ is an 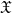$\mathfrak{X}$-group.

Keywords

finite groupsprimitive subgroupssolvable PST-groupsT0-groups

MSC classification

Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D15: Nilpotent groups, $p$-groups 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 373 - 378
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Agrawal, R. K., ‘Finite groups whose subnormal subgroups permute with all Sylow subgroups’, Proc. Amer. Math. Soc. 47 (1975), 77–83.Google Scholar
Asaad, M., Ballester-Bolinches, A. and Esteban-Romero, R., Products of Finite Groups, de Gruyter Expositions in Mathematics, 53 (Walter de Gruyter, Berlin, 2010).Google Scholar
Ballester-Bolinches, A., Beidleman, J. C. and Esteban-Romero, R., ‘On some classes of supersoluble groups’, J. Algebra 312 (1) (2007), 445–454.CrossRefGoogle Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Pedraza-Aguilera, M. C., ‘On a class of $p$-soluble groups’, Algebra Colloq. 12 (2) (2005), 263–267.CrossRefGoogle Scholar
Bray, H. G., Deskins, W. E., Johnson, D., Humphreys, J. F., Puttaswamaiah, B. M., Venzke, P. and Walls, G. L., Between Nilpotent and Solvable (ed. Weinstein, M.) (Polygonal, Washington, NJ, 1982).Google Scholar
Guo, W., Shum, K. P. and Skiba, A., ‘On primitive subgroups of finite groups’, Indian J. Pure Appl. Math. 37 (6) (2006), 369–376.Google Scholar
He, X., Qiao, S. and Wang, Y., ‘A note on primitive subgroups of finite groups’, Commun. Korean Math. Soc. 28 (1) (2013), 55–62.CrossRefGoogle Scholar
Holmes, C. V., ‘Classroom notes: a characterization of finite nilpotent groups’, Amer. Math. Monthly 73 (10) (1966), 1113–1114.Google Scholar
Humphreys, J. F., ‘On groups satisfying the converse of Lagrange’s theorem’, Proc. Cambridge Philos. Soc. 75 (1974), 25–32.CrossRefGoogle Scholar
Johnson, D. L., ‘A note on supersoluble groups’, Canad. J. Math. 23 (1971), 562–564.Google Scholar
Ore, O., ‘Contributions to the theory of groups of finite order’, Duke Math. J. 5 (2) (1939), 431–460.Google Scholar
Ragland, M. F., ‘Generalizations of groups in which normality is transitive’, Comm. Algebra 35 (10) (2007), 3242–3252.Google Scholar
Robinson, D. J. S., A Course in the Theory of Groups, 2nd edn, Graduate Texts in Mathematics, 80 (Springer, New York, 1996).Google Scholar
van der Waall, R. W. and Fransman, A., ‘On products of groups for which normality is a transitive relation on their Frattini factor groups’, Quaest. Math. 19 (1–2) (1996), 59–82.CrossRefGoogle Scholar
Zappa, G., ‘Remark on a recent paper of O. Ore’, Duke Math. J. 6 (1940), 511–512.Google Scholar