Article contents
Polynomials and functions with finite spectra on locally compact Abelian groups
Published online by Cambridge University Press: 17 April 2009
Abstract
In this paper we define polynomials on a locally compact Abelian group G and prove the equivalence of our definition with that of Domar. We explore the properties of polynomials and determine their spectra. We also characterise the primary ideals of certain Beurling algebras 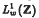 on the group of integers Z. This allows us to classify those elements of
on the group of integers Z. This allows us to classify those elements of 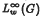 that have finite spectrum. If ϕ is a uniformly continuous function with bounded differences then there is a Beurling algebra naturally associated with ϕ. We give a condition on the spectrum of ϕ relative to this algebra which ensures that ϕ is bounded. Finally we give spectral conditions on a bounded function on ℝ that ensure that its indefinite integral is bounded.
that have finite spectrum. If ϕ is a uniformly continuous function with bounded differences then there is a Beurling algebra naturally associated with ϕ. We give a condition on the spectrum of ϕ relative to this algebra which ensures that ϕ is bounded. Finally we give spectral conditions on a bounded function on ℝ that ensure that its indefinite integral is bounded.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1995
References
- 7
- Cited by


