No CrossRef data available.
Article contents
THE 
$p$-HARMONIC BOUNDARY AND 
${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
Published online by Cambridge University Press: 12 June 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let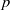 
$p$ be a real number greater than one and let 
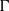$\Gamma $ be a graph of bounded degree. We investigate links between the 
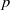$p$-harmonic boundary of 
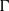$\Gamma $ and the 
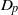${D}_{p} $-massive subsets of 
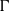$\Gamma $. In particular, if there are 
$n$ pairwise disjoint 
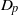${D}_{p} $-massive subsets of 
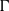$\Gamma $, then the 
$p$-harmonic boundary of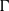 
$\Gamma $ consists of at least 
$n$ elements. We show that the converse of this statement is also true.
Keywords
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 149 - 158
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Cantón, A., Fernández, J. L., Pestana, D. and Rodríguez, J. M., ‘On harmonic functions on trees’, Potential Anal. 15 (3) (2001), 199–244.Google Scholar
Holopainen, I. and Soardi, P. M., ‘
$p$-harmonic functions on graphs and manifolds’, Manuscripta Math. 94 (1) (1997), 95–110.Google Scholar
$p$-harmonic functions on graphs and manifolds’, Manuscripta Math. 94 (1) (1997), 95–110.Google ScholarHolopainen, I. and Soardi, P. M., ‘A strong Liouville theorem for $p$-harmonic functions on graphs’, Ann. Acad. Sci. Fenn. Math. 22 (1) (1997), 205–226.Google Scholar
$p$-harmonic functions on graphs’, Ann. Acad. Sci. Fenn. Math. 22 (1) (1997), 205–226.Google ScholarKanai, M., ‘Rough isometries, and combinatorial approximations of geometries of noncompact Riemannian manifolds’, J. Math. Soc. Japan 37 (3) (1985), 391–413.CrossRefGoogle Scholar
Kanai, M., ‘Rough isometries and the parabolicity of Riemannian manifolds’, J. Math. Soc. Japan 38 (2) (1986), 227–238.CrossRefGoogle Scholar
Kaufman, R., Llorente, J. G. and Wu, J.-M., ‘Nonlinear harmonic measures on trees’, Ann. Acad. Sci. Fenn. Math. 28 (2) (2003), 279–302.Google Scholar
Kayano, T. and Yamasaki, M., ‘Boundary limit of discrete Dirichlet potentials’, Hiroshima Math. J. 14 (2) (1984), 401–406.Google Scholar
Kim, S. W. and Lee, Y. H., ‘Positive $p$-harmonic functions on graphs’, Bull. Korean Math. Soc. 42 (2) (2005), 421–432.CrossRefGoogle Scholar
$p$-harmonic functions on graphs’, Bull. Korean Math. Soc. 42 (2) (2005), 421–432.CrossRefGoogle ScholarKim, S. W. and Lee, Y. H., ‘Energy finite $p$-harmonic functions on graphs and rough isometries’, Commun. Korean Math. Soc. 22 (2) (2007), 277–287.CrossRefGoogle Scholar
$p$-harmonic functions on graphs and rough isometries’, Commun. Korean Math. Soc. 22 (2) (2007), 277–287.CrossRefGoogle ScholarPuls, M. J., ‘The first ${L}^{p} $-cohomology of some finitely generated groups and $p$-harmonic functions’, J. Funct. Anal. 237 (2) (2006), 391–401.Google Scholar
${L}^{p} $-cohomology of some finitely generated groups and 
$p$-harmonic functions’, J. Funct. Anal. 237 (2) (2006), 391–401.Google ScholarPuls, M. J., ‘Graphs of bounded degree and the $p$-harmonic boundary’, Pacific J. Math. 248 (2) (2010), 429–452.Google Scholar
$p$-harmonic boundary’, Pacific J. Math. 248 (2) (2010), 429–452.Google ScholarPuls, M. J., ‘Some results concerning the $p$-Royden and $p$-harmonic boundaries of a graph of bounded degree’, Ann. Acad. Sci. Fenn. Math. 37 (2012), 81–90.Google Scholar
$p$-Royden and 
$p$-harmonic boundaries of a graph of bounded degree’, Ann. Acad. Sci. Fenn. Math. 37 (2012), 81–90.Google ScholarSario, L. and Nakai, M., Classification theory of Riemann surfaces, Die Grundlehren der mathematischen Wissenschaften, 164 (Springer, New York, 1970).Google Scholar
Shanmugalingam, N., ‘Some convergence results for $p$-harmonic functions on metric measure spaces’, Proc. Lond. Math. Soc. (3) 87 (1) (2003), 226–246.CrossRefGoogle Scholar
$p$-harmonic functions on metric measure spaces’, Proc. Lond. Math. Soc. (3) 87 (1) (2003), 226–246.CrossRefGoogle ScholarSoardi, P. M., Potential theory on infinite networks, Lecture Notes in Mathematics, 1590 (Springer, Berlin, 1994).CrossRefGoogle Scholar
Wysoczański, J., ‘Royden compactification of integers’, Hiroshima Math. J. 26 (3) (1996), 515–529.CrossRefGoogle Scholar
Yamasaki, M., ‘Parabolic and hyperbolic infinite networks’, Hiroshima Math. J. 7 (1) (1977), 135–146.CrossRefGoogle Scholar
Yamasaki, M., ‘Ideal boundary limit of discrete Dirichlet functions’, Hiroshima Math. J. 16 (2) (1986), 353–360.CrossRefGoogle Scholar
You have
Access