Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-09T20:13:30.794Z Has data issue: false hasContentIssue false
  • English
  • Français

The Perimeter of optimal convex lattice polygons in the sense of different metrics

Published online by Cambridge University Press:  17 April 2009

Miloš Stojaković
Miloš Stojaković
Affiliation:
Institute of Mathematics, Faculty of Science, University of Novi SadTrg D. Obradovića 4, 21000 Novi Sad, Yugoslavia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Classes of convex lattice polygons which have minimal lp-perimeter with respect to the number of their vertices are said to be optimal in the sense of the lp-metric.

It is proved that if p and q are arbitrary integers or ∞, the asymptotic expression for the lq-perimeter of these optimal convex lattice polygons Qp(n) as a function of the number of their vertices n is 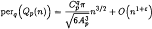. for arbitrary ɛ > 0, where 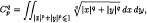. and Ap is equal to the area of the planar shape |x|p + |y|p ≤ 1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 63 , Issue 2 , April 2001 , pp. 229 - 242
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Acketa, D.M. and Žunić, J. ‘On the maximal number of edges of convex digital polygons included into a m × m-grid’, J. Combin. Theory Ser. A 69 (1995), 358–368.CrossRefGoogle Scholar
[2]Apostol, T.M., Introduction to analytic number theory (Springer-Verlag, Berlin, Heidelberg, New York, 1976).Google Scholar
[3]Bombieri, E. and Pila, J., ‘The number of integral points on arcs and ovals’, Duke Math. J. 59 (1989), 337–357.CrossRefGoogle Scholar
[4]Colburn, J.C. and Simpson, R.J., ‘A note on bounds on the minimum area of convex lattice polygons’, Bull. Austral. Math. Soc. 45 (1992), 237–240.CrossRefGoogle Scholar
[5]Jarnik, V., ‘Über die Gitterpunkte auf konvexen Kurven’, Math. Z. 24 (1925), 500–518.CrossRefGoogle Scholar
[6]Matić-Kekić, S., Acketa, D.M. and Žunić, J., ‘An exact construction of digital convex polygons with minimal diameter’, Discrete Math. 150 (1996), 303–313.CrossRefGoogle Scholar
[7]Schmidt, W.M., ‘Integer points on curves and surfaces’, Monatsh. Math. 99 (1985), 45–72.CrossRefGoogle Scholar
[8]Swinerton-Dyer, H.P.F., ‘The number of lattice points on a convex curve’, J. Number Theory 6 (1974), 128–135.CrossRefGoogle Scholar
[9]Žunić, J. ‘Extremal problems on convex lattice polygons in sense of lp-metrics’, (private communication).Google Scholar
[10]Žunić, J. ‘Notes on optimal convex lattice polygons’, Bull. London Math. Soc. 30 (1998), 377–385.CrossRefGoogle Scholar