Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mahler, Kurt
1976.
On the transcendency of the solutions of a special class of functional equations: Corrigendum.
Bulletin of the Australian Mathematical Society,
Vol. 14,
Issue. 3,
p.
477.
Loxton, J.H.
and
van der Poorten, A.J.
1977.
Arithmetic properties of certain functions in several variables III.
Bulletin of the Australian Mathematical Society,
Vol. 16,
Issue. 1,
p.
15.
Gould, H.W.
1977.
A Rearrangement of Series Based on a Partition of the Natural Numbers.
The Fibonacci Quarterly,
Vol. 15,
Issue. 1,
p.
67.
Galochkin, A. I.
1980.
Transcendence measure of values of functions satisfying certain functional equations.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 27,
Issue. 2,
p.
83.
Mahler, K
1982.
Fifty years as a mathematician.
Journal of Number Theory,
Vol. 14,
Issue. 2,
p.
121.
Badea, C.
1987.
The irrationality of certain infinite series.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 2,
p.
221.
Nyblom, M.A.
2000.
A Theorem on Transcendence of Infinite Series.
Rocky Mountain Journal of Mathematics,
Vol. 30,
Issue. 3,
Nyblom, M.A.
2001.
A Theorem on Transcendence of Infinite Series II.
Journal of Number Theory,
Vol. 91,
Issue. 1,
p.
71.
Masser, David
2003.
Diophantine Approximation.
Vol. 1819,
Issue. ,
p.
1.
Nyblom, M.A.
2004.
An extension of a result of Sierpiński.
Journal of Number Theory,
Vol. 105,
Issue. 1,
p.
49.
Kurosawa, Takeshi
2007.
Transcendence of certain series involving binary linear recurrences.
Journal of Number Theory,
Vol. 123,
Issue. 1,
p.
35.
Nguyen, Khoa Dang
2022.
Transcendental series of reciprocals of Fibonacci and Lucas numbers.
Algebra & Number Theory,
Vol. 16,
Issue. 7,
p.
1627.


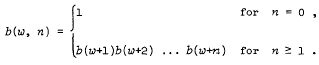
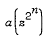 for
for