Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:15:51.240Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE TOTAL DISTANCE AND DIAMETER OF GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  03 May 2018

HONGBO HUA Open the ORCID record for HONGBO HUA [Opens in a new window]
HONGBO HUA*
Affiliation:
Faculty of Mathematics and Physics, Huaiyin Institute of Technology, Huaian, Jiangsu 223003, PR China email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The total distance (or Wiener index) of a connected graph 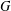$G$ is the sum of all distances between unordered pairs of vertices of 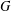$G$. DeLaViña and Waller [‘Spanning trees with many leaves and average distance’, Electron. J. Combin.15(1) (2008), R33, 14 pp.] conjectured in 2008 that if 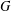$G$ has diameter 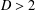$D>2$ and order 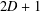$2D+1$, then the total distance of 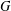$G$ is at most the total distance of the cycle of the same order. In this note, we prove that this conjecture is true for 2-connected graphs.

Keywords

total distancediameter2-connected graphs

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 05C35: Extremal problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 14 - 17
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Aouchiche, M., Bonnefoy, J. M., Fidahoussen, A., Caporossi, G., Hansen, P., Hiesse, L., Lachere, J. and Monhait, A., ‘Variable neighborhood search for extremal graphs. 14. The AutoGraphiX 2 system’, in: Global Optimization: From Theory to Implementation (eds. Liberti, L. and Maculan, N.) (Springer, New York, 2006), 281–310.CrossRefGoogle Scholar
Bonchev, D., ‘The Wiener number – some applications and new developments’, in: Topology in Chemistry: Discrete Mathematics of Molecules (eds. Rouvray, D. H. and King, R. B.) (Horwood, Chichester, 2002), 58–88.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory with Applications (Macmillan, London; Elsevier, New York, 1976).CrossRefGoogle Scholar
DeLaViña, E. and Waller, B., ‘Spanning trees with many leaves and average distance’, Electron. J. Combin. 15(1) (2008), R33, 14 pp.CrossRefGoogle Scholar
Fajtlowicz, S. and Waller, W. A., ‘On two conjectures of GRAFFITI II’, Congr. Numer. 60 (1987), 187–197.Google Scholar
Hua, H., Chen, Y. and Das, K. Ch., ‘The difference between remoteness and radius of a graph’, Discrete Appl. Math. 187 (2015), 103–110.CrossRefGoogle Scholar
Menger, K., ‘Zur allgemeinen Kurventheorie’, Fund. Math. 10 (1927), 96–115.Google Scholar
Plesnik, J., ‘On the sum of all distances in a graph or digraph’, J. Graph Theory 8 (1984), 1–24.CrossRefGoogle Scholar