Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T17:13:08.037Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE REGULAR GRAPH RELATED TO THE G-CONJUGACY CLASSES

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  12 May 2021

ADAM B. R. Open the ORCID record for ADAM B. R. [Opens in a new window]  and
Z. AKHLAGHI Open the ORCID record for Z. AKHLAGHI [Opens in a new window]
ADAM B. R.
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 15914 Tehran, Iran e-mail: [email protected]
Z. AKHLAGHI*
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 15914 Tehran, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5746, Tehran, Iran
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite group G with a normal subgroup N, the simple graph 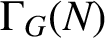$\Gamma _{\textit {G}}( \textit {N} )$ is a graph whose vertices are of the form 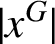$|x^G|$ , where 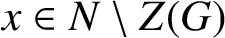$x\in {N\setminus {Z(G)}}$ and 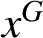$x^G$ is the G-conjugacy class of N containing the element x. Two vertices 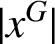$|x^G|$ and 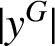$|y^G|$ are adjacent if they are not coprime. We prove that, if 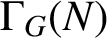$\Gamma _G(N)$ is a connected incomplete regular graph, then 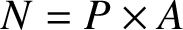$N= P \times {A}$ where P is a p-group, for some prime p, 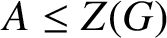$A\leq {Z(G)}$ and 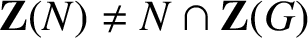$\textbf {Z}(N)\not = N\cap \textbf {Z}(G)$ .

Keywords

finite groupG-conjugacy class sizesregular graph

MSC classification

Primary: 20E45: Conjugacy classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 101 - 105
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the second author was in part supported by a grant from IPM (No. 1400200028).

References

Beltrán, A., Felipe, M. J. and Melchor, C., ‘Graphs associated to conjugacy classes of normal subgroups in finite groups’, J. Algebra 443 (2015), 335–348.CrossRefGoogle Scholar
Bertram, E. A., Herzog, M. and Mann, A., ‘On a graph related to conjugacy classes of groups’, Bull. Lond. Math. Soc. 22(6) (1990), 569–575.CrossRefGoogle Scholar
Bianchi, M., Camina, R. D., Herzog, M. and Pacifici, E., ‘Conjugacy classes of finite groups and graph regularity’, Forum Math. 27(6) (2015), 3167–3172.CrossRefGoogle Scholar
Bianchi, M., Herzog, M., Pacifici, E. and Saffirio, G., ‘On the regularity of a graph related to conjugacy classes of groups’, European J. Combin. 33(7) (2012), 1402–1407.CrossRefGoogle Scholar
Camina, A. R. and Camina, R. D., ‘The influence of conjugacy class sizes on the structure of finite groups: a survey’, Asian-Eur. J. Math. 4(4) (2011), 559–588.CrossRefGoogle Scholar
Lewis, M. L., ‘An overview of graphs associated with character degrees and conjugacy class sizes in finite groups’, Rocky Mountain J. Math. 38 (2008), 175–211.CrossRefGoogle Scholar