ON THE REAL-VALUED GENERAL SOLUTIONS OF THE D’ALEMBERT EQUATION WITH INVOLUTION

Abstract

We find all real-valued general solutions 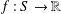$f:S\rightarrow \mathbb{R}$ of the d’Alembert functional equation with involution

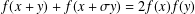$$\begin{eqnarray}\displaystyle f(x+y)+f(x+\unicode[STIX]{x1D70E}y)=2f(x)f(y) & & \displaystyle \nonumber\end{eqnarray}$$

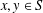for all $x,y\in S$, where 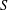$S$ is a commutative semigroup and 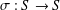$\unicode[STIX]{x1D70E}~:~S\rightarrow S$ is an involution. Also, we find the Lebesgue measurable solutions 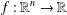$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the above functional equation, where 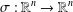$\unicode[STIX]{x1D70E}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ is a Lebesgue measurable involution. As a direct consequence, we obtain the Lebesgue measurable solutions 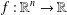$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the classical d’Alembert functional equation

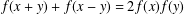$$\begin{eqnarray}\displaystyle f(x+y)+f(x-y)=2f(x)f(y) & & \displaystyle \nonumber\end{eqnarray}$$

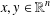for all $x,y\in \mathbb{R}^{n}$. We also exhibit the locally bounded solutions 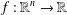$f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ of the above equations.