Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T19:05:52.140Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ORDER OF ARC-STABILISERS IN ARC-TRANSITIVE GRAPHS, II

Part of: Permutation groups

Published online by Cambridge University Press:  02 August 2012

GABRIEL VERRET
GABRIEL VERRET*
Affiliation:
FAMNIT, University of Primorska, Glagoljaška 8, 6000 Koper, Slovenia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

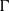Let $\Gamma $ be a 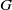$G$-vertex-transitive graph and let 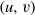$(u,v)$ be an arc of $\Gamma $. It is known that if the local action 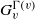$G_v^{\Gamma (v)}$ (the permutation group induced by 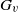$G_v$ on 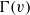$\Gamma (v)$) is permutation isomorphic to the dihedral group of degree four, then either 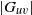$|G_{uv}|$ is ‘small’ with respect to the order of 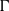$\Gamma $ or 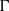$\Gamma $is one of a family of well-understood graphs. In this paper, we generalise this result to a wider class of local actions.

Keywords

arc-transitive graphsgraph-restrictive grouplocal action

MSC classification

Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 441 - 447
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Glauberman, G., ‘Normalizers of $p$-subgroups in finite groups’, Pacific J. Math. 29 (1969), 137–144.CrossRefGoogle Scholar
[2]Potočnik, P., Spiga, P. & Verret, G., ‘On graph-restrictive permutation groups’, J. Combin. Theory Ser. B 102 (2012), 820–831.CrossRefGoogle Scholar
[3]Potočnik, P., Spiga, P. & Verret, G., ‘Bounding the order of the vertex-stabiliser in $3$-valent vertex-transitive and $4$-valent arc-transitive graphs’, arXiv:1010.2546v1 [math.CO].Google Scholar
[4]Praeger, C. E. & Xu, M. Y., ‘A characterization of a class of symmetric graphs of twice prime valency’, European J. Combin. 10 (1989), 91–102.CrossRefGoogle Scholar
[5]Tutte, W. T., ‘A family of cubical graphs’, Proc. Cambridge Philos. Soc. 43 (1947), 459–474.CrossRefGoogle Scholar
[6]Tutte, W. T., ‘On the symmetry of cubic graphs’, Canad. J. Math. 11 (1959), 621–624.CrossRefGoogle Scholar
[7]Verret, G., ‘On the order of arc-stabilizers in arc-transitive graphs’, Bull. Aust. Math. Soc. 80 (2009), 498–505.CrossRefGoogle Scholar