Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Albrecht, Martin
Bai, Shi
and
Ducas, Léo
2016.
Advances in Cryptology – CRYPTO 2016.
Vol. 9814,
Issue. ,
p.
153.
Huck, Christian
2018.
Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics.
Vol. 2213,
Issue. ,
p.
249.
Ferraguti, Andrea
2018.
The set of stable primes for polynomial sequences with large Galois group.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 7,
p.
2773.
SITTINGER, BRIAN D.
2018.
THE DENSITY OF -WISE RELATIVELY -PRIME ALGEBRAIC INTEGERS.
Bulletin of the Australian Mathematical Society,
Vol. 98,
Issue. 2,
p.
221.
Lieb, Julia
2018.
Uniform probability and natural density of mutually left coprime polynomial matrices over finite fields.
Linear Algebra and its Applications,
Vol. 539,
Issue. ,
p.
134.
Micheli, Giacomo
and
Weger, Violetta
2019.
On Rectangular Unimodular Matrices over the Algebraic Integers.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 1,
p.
425.
Bostan, Alin
Marynych, Alexander
and
Raschel, Kilian
2019.
On the least common multiple of several random integers.
Journal of Number Theory,
Vol. 204,
Issue. ,
p.
113.
Fernández, José L.
and
Fernández, Pablo
2021.
Divisibility properties of random samples of integers.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 1,
Martineau, Sébastien
2022.
On coprime percolation, the visibility graphon, and the local limit of the GCD profile.
Electronic Communications in Probability,
Vol. 27,
Issue. none,
Micheli, Giacomo
Schraven, Severin
and
Weger, Violetta
2022.
A local to global principle for expected values.
Journal of Number Theory,
Vol. 238,
Issue. ,
p.
1.
Micheli, Giacomo
Schraven, Severin
Tinani, Simran
and
Weger, Violetta
2023.
Geometric sieve over number fields for higher moments.
Research in Number Theory,
Vol. 9,
Issue. 3,
Sittinger, Brian D.
and
Chen, Vickie V.
2024.
The density of tuples restricted by relativelyr-prime conditions.
Miskolc Mathematical Notes,
Vol. 25,
Issue. 1,
p.
465.
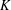 $K$ be a number field with ring of integers
$K$ be a number field with ring of integers 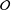 ${\mathcal{O}}$. After introducing a suitable notion of density for subsets of
${\mathcal{O}}$. After introducing a suitable notion of density for subsets of 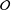 ${\mathcal{O}}$, generalising the natural density for subsets of
${\mathcal{O}}$, generalising the natural density for subsets of 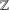 $\mathbb{Z}$, we show that the density of the set of coprime
$\mathbb{Z}$, we show that the density of the set of coprime 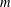 $m$-tuples of algebraic integers is
$m$-tuples of algebraic integers is 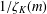 $1/{\it\zeta}_{K}(m)$, where
$1/{\it\zeta}_{K}(m)$, where 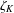 ${\it\zeta}_{K}$ is the Dedekind zeta function of
${\it\zeta}_{K}$ is the Dedekind zeta function of 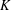 $K$. This generalises a result found independently by Mertens [‘Ueber einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338] and Cesàro [‘Question 75 (solution)’, Mathesis 3 (1883), 224–225] concerning the density of coprime pairs of integers in
$K$. This generalises a result found independently by Mertens [‘Ueber einige asymptotische Gesetze der Zahlentheorie’, J. reine angew. Math. 77 (1874), 289–338] and Cesàro [‘Question 75 (solution)’, Mathesis 3 (1883), 224–225] concerning the density of coprime pairs of integers in 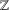 $\mathbb{Z}$.
$\mathbb{Z}$.