Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-14T23:37:13.320Z Has data issue: false hasContentIssue false
  • English
  • Français

On the invariance of certain estimators

Published online by Cambridge University Press:  17 April 2009

J.E. Gentle  and
V.A. Sposito
J.E. Gentle
Affiliation:
Department of Statistics, Iowa State University, Ames, Iowa, USA.
V.A. Sposito
Affiliation:
Department of Statistics, Iowa State University, Ames, Iowa, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, Lp estimators for the parameters in the linear model y = Xβ are considered. In particular, it is shown that these estimators are invariant under scale transformations on the dependent variable; that is, if 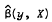is an Lp estimator for β, then 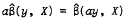for any nonzero scalar a. It is shown that this result does not extend to more general transformations on y, and the invariance property does not hold for general nonlinear models.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 14 , Issue 3 , June 1976 , pp. 405 - 408
Copyright
Copyright © Australian Mathematical Society 1976

References

[1]Appa, Gautam and Smith, Cyril, “On L1 and Chebyshev estimation”, Math. Programming 5 (1973), 73–84.CrossRefGoogle Scholar
[2]Barrodale, I. and Roberts, F.D.K., “An improved algorithm for discrete l 1 linear approximation”, SIAM J. Numer. Anal. 10 (1973), 839–848.CrossRefGoogle Scholar
[3]Barrodale, I. and Roberts, F.D.K., “Applications of mathematical programming to l p approximation”, Nonlinear programming, 447–464 (Proc. Sympos. Mathematics Research Center, University of Wisconsin, Madison, 1970. Academic Press, New York, London, 1970).CrossRefGoogle Scholar
[4]Barrodale, I., Roberts, R.D.K. and Hunt, C.R., “Computing best l p approximations by functions nonlinear in one parameter”, Comput. J. 13 (1970), 382–386.Google Scholar
[5]Ekblom, H. and Henriksson, S., “Lp -criteria for the estimation of location parameters”, SIAM J. Appl. Math. 17 (1969), 1130–1141.CrossRefGoogle Scholar
[6]Forsythe, Alan B., “Robust estimation of straight line regression coefficients by minimizing pth power deviations”, Technometries 14 (1972), 159–166.CrossRefGoogle Scholar
[7]Fraser, D.A.S., Nonparametria methods in statistics (John Wiley & Sons, New York, London, Sydney, 1957).Google Scholar
[8]Rice, John R. and White, John S., “Norms for smoothing and estimation”, SIAM Rev. 6 (1964), 243–256.Google Scholar
[9]Wagner, Harvey M., “Linear programming techniques for regression analysis”, J. Amer. Statist. Assoc. 54 (1959), 206–212.CrossRefGoogle Scholar