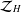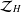Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aljuaid, Munirah
and
Bakhit, Mahmoud Ali
2023.
Composition operators from harmonic $ \mathcal{H}^{\infty} $ space into harmonic Zygmund space.
AIMS Mathematics,
Vol. 8,
Issue. 10,
p.
23087.
Aljuaid, Munirah
and
Colonna, Flavia
2023.
Recent Advances in Mathematical Analysis.
p.
69.
Aljuaid, Munirah
Bakhit, M. A.
and
Ho, Kwok-Pun
2023.
On Characterizations of Weighted Harmonic Bloch Mappings and Its Carleson Measure Criteria.
Journal of Function Spaces,
Vol. 2023,
Issue. ,
p.
1.
Abbasi, Ebrahim
Colonna, Flavia
and
Hassanlou, Mostafa
2025.
Composition Operators Between Harmonic Bloch-Type Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 48,
Issue. 3,