Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:32:29.489Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXPANSIONS OF REAL NUMBERS IN TWO MULTIPLICATIVELY DEPENDENT BASES

Part of: Discrete mathematics in relation to computer science Elementary number theory

Published online by Cambridge University Press:  01 December 2016

YANN BUGEAUD  and
DONG HAN KIM
YANN BUGEAUD
Affiliation:
IRMA, U.M.R. 7501, Université de Strasbourg et CNRS, 7 rue René Descartes, 67084 Strasbourg, France email [email protected]
DONG HAN KIM*
Affiliation:
Department of Mathematics Education, Dongguk University–Seoul, 30 Pildong-ro 1-gil, Jung-gu, Seoul 04620, Korea email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 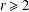$r\geq 2$ and 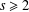$s\geq 2$ be multiplicatively dependent integers. We establish a lower bound for the sum of the block complexities of the $r$-ary expansion and the $s$-ary expansion of an irrational real number, viewed as infinite words on 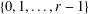$\{0,1,\ldots ,r-1\}$ and 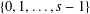$\{0,1,\ldots ,s-1\}$, and we show that this bound is best possible.

Keywords

combinatorics on wordsSturmian wordcomplexityb-ary expansion

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 68R15: Combinatorics on words
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 373 - 383
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Research Foundation of Korea (NRF-2015R1A2A2A01007090) and the research program of Dongguk University, 2016.

References

Allouche, J.-P. and Shallit, J., Automatic Sequences: Theory, Applications, Generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Bugeaud, Y., ‘On the expansions of a real number to several integer bases’, Rev. Mat. Iberoam. 28 (2012), 931–946.CrossRefGoogle Scholar
Bugeaud, Y. and Kim, D. H., ‘On the expansions of real numbers in two integer bases’, Preprint.Google Scholar
Cassaigne, J., ‘Sequences with grouped factors’, in: DLT’97, Developments in Language Theory III (ed. Bozapalidis, S.) (Aristotle University of Thessaloniki, Thessaloniki, 1998), 211–222.Google Scholar
Choe, C. H. and Kim, D. H., ‘The first return time test for pseudorandom numbers’, J. Comput. Appl. Math. 143 (2002), 263–274.CrossRefGoogle Scholar
Fogg, N. P., Substitutions in Dynamics, Arithmetics and Combinatorics, Lecture Notes in Mathematics, 1794 (eds. Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A.) (Springer, Berlin, 2002).Google Scholar
Lothaire, M., Algebraic Combinatorics on Words, Encyclopedia of Mathematics and its Applications, 90 (Cambridge University Press, Cambridge, 2002).Google Scholar
Morse, M. and Hedlund, G. A., ‘Symbolic dynamics II: Sturmian sequences’, Amer. J. Math. 62 (1940), 1–42.Google Scholar