Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-02T19:14:28.308Z Has data issue: false hasContentIssue false
  • English
  • Français

On the equivalence of a countable disjoint class of sets of positive measure and a weaker condition than total σ–finiteness of measures

Published online by Cambridge University Press:  17 April 2009

V. Ficker
V. Ficker
Affiliation:
Department of Mathematics, University of Newcastle, New South Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, S) be a measurable space and S be a σ-algebra of subsets of X. A nonempty class M is said to be a class of null sets if M ⊂ S, M is closed under countable unions of sets and E ∩ F ∈ M whenever E ∈ M and F ∈ S. It is possible to show that such concepts as absolute continuity, singularity and independence of measures can be studied simply by classes of null sets and that similar results can be obtained under the condition that each disjoint subclass of S – M is countable, denoted (S – M)C. If (X, S,μ) is a measure space then M = {E ∈ S: μ(E) = O} is a class of null sets of S and S – M the class of all sets of positive measure. We say that a measure μ has the property σ if there exists a sequence of totally finite measures 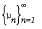on S such that σ(E) = 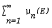for all E ∈ S. This property of measures is weaker than total σ–finiteness of measures. The main result of the present paper is as follows: Let (X, S,μ) be a measure space and M = {E ∈ S: μ(E) = O}. Then (S – M)C if and only if μ has the property σ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 1 , Issue 2 , August 1969 , pp. 237 - 243
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Dunford, Nelson and Schwartz, Jacob T., Linear operators, Part I (Interscience Publishers, New York, London, 1958).Google Scholar
[2]Ficker, V., “Dominated classes and related questions”, Acta Fac. Rerum, Natur. Univ. Comenian. 10, 7 (1966), 3–18.Google Scholar
[3]Halmos, Paul R., Measure theory, (Van Nostrand, New York, 1950).Google Scholar
[4]Neubrunn, Tibor, “Remark on absolute continuity of measures” (Russian) Mat.–Fyz. Časopis Sloven. Akad. Vied. 16 (1966), 21–30.Google Scholar