Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Noye, B.J.
1972.
On the differential equation for the conventional tide-well system.
Bulletin of the Australian Mathematical Society,
Vol. 7,
Issue. 2,
p.
251.


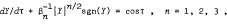
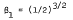 corresponding to critical damping. At the end of the paper, some related equations are considered.
corresponding to critical damping. At the end of the paper, some related equations are considered.