Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T02:33:27.515Z Has data issue: false hasContentIssue false
  • English
  • Français

On the construction of soluble groups satisfying the minimal condition for normal subgroups

Published online by Cambridge University Press:  17 April 2009

Howard L. Silcock
Howard L. Silcock
Affiliation:
Department of Pure Mathematics, University of Adelaide, Adelaide, South Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A general method is described for constructing examples of soluble groups whose normal subgroups form a well-ordered chain under the ordering of inclusion. This method is a variant of one introduced in a recent paper by Heineken and Wilson. Each of the resulting groups is obtained by an embedding procedure from a pair of iterated wreath products A1 wr A2 wr … wr An, B1 wr B2 wr … wr Bn, where the constituent groups Ai., Bi are each either cyclic of prime power order or quasicyclic. Here n may be chosen arbitrarily, and the choice of constituent groups is subject only to a condition on the sequences of prime numbers that may occur as orders of elements in the groups

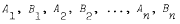
respectively. The construction is applied to give certain examples which illustrate the limitations of results on particular classes of soluble groups satisfying the minimal condition for normal subgroups obtained in recent papers by Hartley, McDougall, and the present author.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 12 , Issue 2 , April 1975 , pp. 231 - 257
Copyright
Copyright © Australian Mathematical Society 1975

References

[1]Hall, P., “Finiteness conditions for soluble groups”, Proc. London Math. Soc. (3) 4 (1954), 419–436.Google Scholar
[2]Hardy, G.H. and Wright, E.M., An introduction to the theory of numbers, 4th ed. (Clarendon Press, Oxford, 1960).Google Scholar
[3]Hartley, B. and McDougall, D., “Injective modules and soluble groups satisfying the minimal condition for normal subgroups”, Bull. Austral. Math. Soc. 4 (1971), 113–135.CrossRefGoogle Scholar
[4]Heineken, H. and Wilson, J.S., “Locally soluble groups with min-n”, J. Austral. Math. Soc. 17 (1974), 305–318.CrossRefGoogle Scholar
[5]McDougall, David, “Soluble groups with the minimum condition for normal subgroups”, Math. Z. 118 (1970), 157–167.CrossRefGoogle Scholar
[6]McDougall, D., “The subnormal structure of some classes of soluble groups”, J. Austral. Math. Soc. 13 (1972), 365–377.CrossRefGoogle Scholar
[7]Neumann, B.H., “Twisted wreath products of groups”, Arch. Math. 14 (1963), 1–6.CrossRefGoogle Scholar
[8]Neumann, Peter M., “On the structure of standard wreath products of groups”, Math. Z. 84 (1964), 343–373.CrossRefGoogle Scholar
[9]Robinson, Derek J.S., Finiteness conditions and generalized soluble groups, Part 1 (Ergebnisse der Mathematik und ihrer Grenzgebiete, 62. Springer-Verlag, Berlin, Heidelberg, New York, 1972).Google Scholar
[10]Robinson, Derek J.S., Finiteness conditions and generalized soluble groups, Part 2 (Ergebnisse der Mathematik und ihrer Grenzgebiete, 63. Springer-Verlag, Berlin, Heidelberg, New York, 1972).Google Scholar
[11]Roseblade, J.E. and Wilson, J.S., “A remark about monolithic groups”, J. London Math. Soc. (2) 3 (1971), 361–362.CrossRefGoogle Scholar
[12]Silcock, Howard L., “Metanilpotent groups satisfying the minimal condition for normal subgroups”, Math. Z. 135 (1974), 165–173.CrossRefGoogle Scholar
[13]Wilson, John S., “Some properties of groups inherited by normal subgroups of finite index”, Math. Z. 114 (1970), 19–21.CrossRefGoogle Scholar