Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T20:38:55.225Z Has data issue: false hasContentIssue false
  • English
  • Français

On the coefficients of transformation polynomials for the modular function

Published online by Cambridge University Press:  17 April 2009

Kurt Mahler
Kurt Mahler
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper (Acta Arith. 21 (1972), 89–97), I had proved that the sum of the absolute values of the coefficients of the mth transformation polynomial Fm (u, v) of the Weber modular function j(ω) of level 1 is not greater than 2(36n+57)2n when m = 2n is a power of 2. The aim of the present paper is to give an analogous bound for the case of general m. This upper bound is much less good and of the form 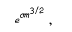where c > 0 is an absolute constant which can be determined effectively. It seems probable that also in the general case an upper bound of the form eO(m10gm) should hold, but I have not so far succeeded in proving such a result.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 10 , Issue 2 , April 1974 , pp. 197 - 218
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Baker, A., “On some diophantine inequalities involving the exponential function”, Canad. J. Math. 17 (1965), 616–626.CrossRefGoogle Scholar
[2]Fueter, R., Vorlesungen über die singulären Moduln und die komplexe Multiplikation der elliptischen Funktionen, Erster Teil (Teubners Sammlung von Lehrbüchern auf dem Gebiete der mathematischen Wissenschaften, Band 41. Verlag und Druck von B.C. Teubner, Leipzig, Berlin, 1924).Google Scholar
[3]Mahler, K., “On some inequalities for polynomials in several variables”, J. London Math. Soc. 37 (1962), 341–344.CrossRefGoogle Scholar
[4]Mahler, Kurt, “On the coefficients of the 2n-th transformation polynomial for j(ω)”, Acta Arith. 21 (1972), 89–97.CrossRefGoogle Scholar