Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T15:08:43.873Z Has data issue: false hasContentIssue false
  • English
  • Français

On the classification of just-non-Cross varieties of groups

Published online by Cambridge University Press:  17 April 2009

J. M. Brady
J. M. Brady
Affiliation:
Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Apart from some (insoluble) subvarieties of 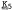, the jnC (just-non-Cross) varieties known so far comprise the following list: 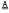, , 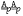, , 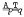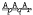where p, q and r are any three distinct primes. In a recent paper I gave a partial confirmation of the conjecture that the soluble jnC varieties all appear in this list. Here I show that a jnC variety is reducible if and only if it is soluble of finite exponent; this reduces the problem of classifying jnC varieties to finding the irreducibles of finite exponent. I observe that these fall into three distinct classes, and show that the questions of whether or not two of these classes are empty have some bearing on some apparently difficult problems of group theory.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 3 , Issue 3 , December 1970 , pp. 293 - 311
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Bachmuth, Seymour, Mochizuki, Horace Y. and Walkup, David, “A nonsolvable group of exponent five”, (to appear).Google Scholar
[2]Brady, J.M., “On soluble just-non-Cross varieties of groups”, Bull. Austral. Math. Soc. 3 (1970), 313–323.CrossRefGoogle Scholar
[3]Cossey, P.J., “On varieties of A-groups”, Ph.D. thesis, Australian National University, 1966. See also Proc. Internat. Conf. Theory of Groups, Austral. Nat. Univ., Canberra, 1965, 71 (Gordon and Breach, New York, 1967).Google Scholar
[4]Curtis, Charles W. and Reiner, Irving, Representation theóry of finite groups and associative algebras (Interscience, New York, 1962).Google Scholar
[5]Hall, P. and Higman, Graham, “On the p–length of p–soluble groups and reduction theorems for Burnside's problem”, Proo. London Math. Soc. (3) 6 (1956), 1–42.Google Scholar
[6]Huppert, Bertram, Endliche Gruppen I (Die Grundlehren der mathematischen Wissenschaften, Band 134, Springer-Verlag, Berlin, Heidelberg, New York, 1967).Google Scholar
[7]Kovács, L.G., “Varieties and finite groups”, J. Austral. Math. Soc. 10 (1969), 5–19.Google Scholar
[8]Kovács, L.G. and Newman, M.F., “Cross varieties of groups”, Proc. Roy. Soc. Ser. A. 292 (1966), 530–536.Google Scholar
[9]Kovács, L.G. and Newman, M.F., “Just non-Cross varieties”, Proc. Intemat. Conf. Theory of Groups, Austral. Nat. Univ., Canberra, 1965, 221–223 (Gordon and Breach, New York, 1967).Google Scholar
[10]Kovács, L.G. and Newman, M.F., “On non-Cross varieties of groups”, J. Austral. Math. Soc. (to appear).Google Scholar
[11]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37, Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[12]Dates, Sheila and Powell, M.B., “Identical relations in finite groups”, J. Algebra 1 (1964), 11–39.Google Scholar
[13]Ol's˘anskii˘, A.Ju., “Varieties of residually finite groups”, (Russian), Izv. Akad. Nauk SSSR Ser. Mat. 33 (1969), 915–927.Google Scholar
[14]Wielandt, Helmut, Finite permutation groups (Academic Press, New York, 1964).Google Scholar