Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T10:00:23.431Z Has data issue: false hasContentIssue false
  • English
  • Français

On the associativity of the torsion functor

Published online by Cambridge University Press:  17 April 2009

John Clark
John Clark
Affiliation:
Department of Mathematics, The University of Otago, Dunedin, New Zealand.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with identity. We say that tor is associative over R if for all R-modules A, B, C there is an isomorphism 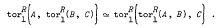Our main results are that (1) tor is associative over a noetherian ring R if and only if R is the direct sum of a finite number of Dedekind rings and uniserial rings, and (2) tor is associative over an integral domain R if and only if R is a Prüfer ring.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 10 , Issue 1 , February 1974 , pp. 107 - 118
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Asano, Keizo, “Über kommutative Ringe, in denen jedes Ideal als Produkt von Primidealen darstellbar ist”, J. Math. Soc. Japan 3 (1951), 82–90.CrossRefGoogle Scholar
[2]Cartan, Henri and Eilenberg, Samuel, Homological algebra (Princeton University Press, Princeton, New Jersey, 1956).Google Scholar
[3]Cohen, I.S. and Kaplansky, I., “Rings for which every module is a direct sum of cyclic modules”, Math. Z. 54 (1951), 97–101.CrossRefGoogle Scholar
[4]Fuchs, Ladislaus, “Über die Ideale arithmetischer Ringe”, Comment. Math. Helv. 23 (1949), 334–341.CrossRefGoogle Scholar
[5]Gilmer, Robert W., Multiplicative ideal theory (Queen's Papers in Pure and Applied Mathematics, 12. Queen's University, Kingston, Ontario, 1968).Google Scholar
[6]Hattori, Akira, “On Prüfer rings”, J. Math. Soc. Japan 9 (1957), 381–385.CrossRefGoogle Scholar
[7]Jensen, Chr. U., “On characterizations of Prüfer rings”, Math. Scand. 13 (1963), 90–98.CrossRefGoogle Scholar
[8]Jensen, C.U., “Arithmetical rings”, Acta Math. Acad. Sci. Hungar. 17 (1966), 115–123.CrossRefGoogle Scholar
[9]Kaplansky, Irving, “Elementary divisors and modules”, Trans. Amer. Math. Soc. 66 (1949), 464–491.CrossRefGoogle Scholar
[10]Kaplansky, Irving, Commutative rings (Anyn and Bacon, Boston, 1970).Google Scholar
[11]Köthe, Gottfried, “Verallgemeinerte Abelsche Gruppen mit hyperkomple hyperkomplexen Operatorenring”, Math. Z. 39 (1935), 31–44 (1934).CrossRefGoogle Scholar
[12]Lambek, Joachim, Lectures on rings and modules (Blaisdell, Waltham, Massachusetts; London; Toronto; 1966).Google Scholar
[13]Northcott, D.G., Ideal theory (Cambridge Tracts in Mathematics and Mathematical Physics, 42. Cambridge University Press, Cambridge, 1953).CrossRefGoogle Scholar
[14]Northcott, D.G., An introduction to homological algebra (Cambridge University Press, Cambridge, 1960).CrossRefGoogle Scholar