Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T03:33:19.421Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ALGEBRAIC CONVERGENCE OF FINITELY GENERATED KLEINIAN GROUPS IN ALL DIMENSIONS

Part of: Riemann surfaces

Published online by Cambridge University Press:  08 December 2011

XI FU
XI FU*
Affiliation:
Department of Mathematics, Shaoxing College of Arts and Sciences, Shaoxing, Zhejiang 312000, PR China (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {Gr,i} be a sequence of r-generator Kleinian groups acting on 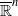. In this paper, we prove that if {Gr,i} satisfies the F-condition, then its algebraic limit group Gr is also a Kleinian group. The existence of a homomorphism from Gr to Gr,i is also proved. These are generalisations of all known corresponding results.

Keywords

Kleinian groupWY(G)loxodromic elementalgebraic convergence

MSC classification

Secondary: 30F40: Kleinian groups 57S30: Discontinuous groups of transformations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 85 , Issue 2 , April 2012 , pp. 275 - 279
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Beardon, A. F., The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91 (Springer, New York, 1983).CrossRefGoogle Scholar
[2]Fang, A. and Nai, B., ‘On the discreteness and convergence in n-dimensional Möbius groups’, J. Lond. Math. Soc. 61 (2000), 761–773.Google Scholar
[3]Jørgensen, T. and Klein, P., ‘Algebraic convergence of finitely generated Kleinian groups’, Q. J. Math. Oxford 33 (1982), 325–332.CrossRefGoogle Scholar
[4]Kapovich, M., ‘On the sequences of finitely generated discrete groups, in the tradition of Ahlfors–Bers. V’, Contemp. Math. 510 (2010), 165–184.CrossRefGoogle Scholar
[5]Martin, G., ‘On discrete Möbius groups in all dimensions: a generalization of Jørgensen’s inequality’, Acta Math. 163 (1989), 253–289.CrossRefGoogle Scholar
[6]Wang, X., ‘Dense subgroups of n-dimensional Möbius groups’, Math. Z. 243 (2003), 643–651.CrossRefGoogle Scholar
[7]Wang, X., ‘Algebraic convergence theorems of n-dimensional Kleinian groups’, Israel J. Math. 162 (2007), 221–233.CrossRefGoogle Scholar
[8]Wang, X. and Yang, W., ‘Discreteness criteria of Möbius groups of high dimensions and convergence theorems of Kleinian groups’, Adv. Math. 159 (2001), 68–82.CrossRefGoogle Scholar
[9]Waterman, P., ‘Möbius transformations in several dimensions’, Adv. Math. 101 (1993), 87–113.CrossRefGoogle Scholar
[10]Yang, S., ‘Algebraic convergence of finitely generated Kleinian groups in all dimensions’, Linear Algebra Appl. 432 (2010), 1147–1151.CrossRefGoogle Scholar