No CrossRef data available.
Article contents
ON STARK’S CLASS NUMBER CONJECTURE AND THE GENERALISED BRAUER–SIEGEL CONJECTURE
Published online by Cambridge University Press: 10 January 2022
Abstract
Stark conjectured that for any
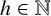 $h\in \Bbb {N}$
, there are only finitely many CM-fields with class number h. Let
$h\in \Bbb {N}$
, there are only finitely many CM-fields with class number h. Let
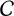 $\mathcal {C}$
be the class of number fields L for which L has an almost normal subfield K such that
$\mathcal {C}$
be the class of number fields L for which L has an almost normal subfield K such that
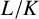 $L/K$
has solvable Galois closure. We prove Stark’s conjecture for
$L/K$
has solvable Galois closure. We prove Stark’s conjecture for
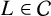 $L\in \mathcal {C}$
of degree greater than or equal to 6. Moreover, we show that the generalised Brauer–Siegel conjecture is true for asymptotically good towers of number fields
$L\in \mathcal {C}$
of degree greater than or equal to 6. Moreover, we show that the generalised Brauer–Siegel conjecture is true for asymptotically good towers of number fields
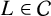 $L\in \mathcal {C}$
and asymptotically bad families of
$L\in \mathcal {C}$
and asymptotically bad families of
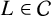 $L\in \mathcal {C}$
.
$L\in \mathcal {C}$
.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 288 - 300
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is currently an NCTS postdoctoral fellow.



