Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T00:47:24.276Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SI-GROUPS

Part of: Abelian groups Modules, bimodules and ideals

Published online by Cambridge University Press:  12 September 2014

R. R. ANDRUSZKIEWICZ  and
M. WORONOWICZ
R. R. ANDRUSZKIEWICZ
Affiliation:
Institute of Mathematics, University of Białystok, 15-267 Białystok, Akademicka 2,Poland email [email protected]
M. WORONOWICZ*
Affiliation:
Institute of Mathematics, University of Białystok, 15-267 Białystok, Akademicka 2, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents new results concerning the structure of 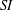$\text{SI}$-groups and refines and purifies the results obtained in this field by Shalom Feigelstock [‘Additive groups of rings whose subrings are ideals’, Bull. Aust. Math. Soc.55 (1997), 477–481]. The structure theorem describing torsion-free 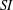$\text{SI}$-groups is proved in the associative case. Numerous examples of 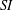$\text{SI}$-groups are given. Some inconsistencies in Feigelstock’s article are noted and corrected.

Keywords

SI-groupsH-ringsidealstorsion-free groupsassociative ring multiplication

MSC classification

Primary: 20K99: None of the above, but in this section
Secondary: 16D25: Ideals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 92 - 103
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aghdam, A. M., ‘Square subgroup of an Abelian group’, Acta Sci. Math. 51 (1987), 343–348.Google Scholar
Aghdam, A. M. and Najafizadeh, A., ‘Square subgroups of rank two Abelian groups’, Colloq. Math. 117(1) (2009), 19–28.Google Scholar
Aghdam, A. M. and Najafizadeh, A., ‘Square submodule of a module’, Mediterr. J. Math. 7(2) (2010), 195–207.CrossRefGoogle Scholar
Aghdam, A. M., Karimi, F. and Najafizadeh, A., ‘On the subgroups of torsion-free groups which are subrings in every ring’, Ital. J. Pure Appl. Math. 31 (2013), 63–76.Google Scholar
Andrijanov, V. I., ‘Periodic hamiltonian rings’, Mat. Sb. 74(116) (1967), 241–261; (in Russian); English transl. Mat. Sb. 74(116) No. 2 (1967), 225–241.Google Scholar
Andruszkiewicz, R. R. and Woronowicz, M., ‘On associative ring multiplication on abelian mixed groups’, Comm. Algebra 42(9) (2014), 3760–3767.CrossRefGoogle Scholar
Feigelstock, S., ‘Additive groups of rings whose subrings are ideals’, Bull. Aust. Math. Soc. 55 (1997), 477–481.Google Scholar
Fuchs, L., Infinite Abelian Groups, Vol. 1 (Academic Press, New York, 1970).Google Scholar
Fuchs, L., Infinite Abelian Groups, Vol. 2 (Academic Press, New York, 1973).Google Scholar
Kruse, R. L., ‘Rings in which all subrings are ideals’, Canad. J. Math. 20 (1968), 862–871.Google Scholar
Rédei, L., ‘Vollidealringe im weiteren Sinn. I’, Acta Math. Acad. Sci. Hungar. 3 (1952), 243–268.Google Scholar