No CrossRef data available.
Article contents
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
Published online by Cambridge University Press: 17 November 2021
Abstract
We investigate, for given positive integers a and b, the least positive integer
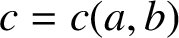$c=c(a,b)$
such that the quotient
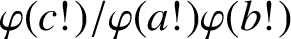$\varphi (c!\kern-1.2pt)/\varphi (a!\kern-1.2pt)\varphi (b!\kern-1.2pt)$
is an integer. We derive results on the limit of
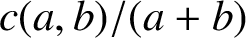$c(a,b)/(a+b)$
as a and b tend to infinity and show that
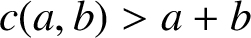$c(a,b)>a+b$
for all pairs of positive integers
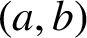$(a,b)$
, with the exception of a set of density zero.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Baczkowski, D., Filaseta, M., Luca, F. and Trifonov, O., ‘On values of
$d\left(n!\right)/ m!$
,
$\phi \left(n!\right)/ m!$
and
$\sigma \left(n!\right)/ m!$
’, Int. J. Number Theory 6(6) (2010), 1199–1214.CrossRefGoogle Scholar
$d\left(n!\right)/ m!$
,
$\phi \left(n!\right)/ m!$
and
$\sigma \left(n!\right)/ m!$
’, Int. J. Number Theory 6(6) (2010), 1199–1214.CrossRefGoogle ScholarErdős, P., Graham, R. L., Ruzsa, I. Z. and Straus, E. G., ‘On the prime factors of
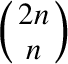$\left(\genfrac{}{}{0pt}{}{2n}{n}\right)$
’, Math. Comp. 29 (1975), 83–92.CrossRefGoogle Scholar
$\left(\genfrac{}{}{0pt}{}{2n}{n}\right)$
’, Math. Comp. 29 (1975), 83–92.CrossRefGoogle ScholarLuca, F., ‘Fibonacci numbers with the Lehmer property’, Bull. Pol. Acad. Sci. Math. 55(1) (2007), 7–15.CrossRefGoogle Scholar
Luca, F. and Shparlinski, I. E., ‘Arithmetic functions with linear recurrence sequences’, J. Number Theory 125(2) (2007), 459–472.CrossRefGoogle Scholar
Luca, F. and Stănică, P., ‘On the Euler function of the Catalan numbers’, J. Number Theory 132(7) (2012), 1404–1424.Google Scholar
Luca, F. and Stănică, P., ‘Monotonic phinomial coefficients’, Bull. Aust. Math. Soc. 95(3) (2017), 365–372.CrossRefGoogle Scholar