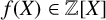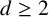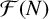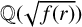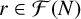ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS

Abstract

Let $f(X) \in {\mathbb Z}[X]$ be a polynomial of degree $d \ge 2$ without multiple roots and let ${\mathcal F}(N)$ be the set of Farey fractions of order N. We use bounds for some new character sums and the square-sieve to obtain upper bounds, pointwise and on average, on the number of fields ${\mathbb Q}(\sqrt {f(r)})$ for $r\in {\mathcal F}(N)$, with a given discriminant.

1 Introduction

1.1 Motivation

Since the work of Shanks [14], there have been many investigations of properties of quadratic fields ${\mathbb Q}(\sqrt {a})$ , for $a\in {\mathcal A}$ , where ${\mathcal A}$ is some sequence of arithmetic interest, including values of exponential polynomials [1, 12, 13, 16, 17], coordinates of integer points on algebraic curves [2–4, 6] and polynomial values [5, 11]. Kulkarni and Levin [10] considered statistical properties of quadratic fields ${\mathbb Q}(\sqrt {f(r)})$ generated by polynomials $f(X) \in {\mathbb Z}[X]$ evaluated at rational points.

To define the quantities of interest, for an integer N, we denote by ${\mathcal F}(N)$ the set of all Farey fractions of order N and their reciprocals, that is,

$$ \begin{align*} {\mathcal F}(N) = \{a/b:~ a,b \in \{0, \ldots, N\}, \ b \ne 0, \ \gcd(a,b)=1\}. \end{align*} $$

Given a nonconstant polynomial $f(X) \in {\mathbb Z}[X]$ of degree d without multiple roots, we denote by ${\mathcal R}_f(N)$ the set of discriminants of the quadratic fields ${\mathbb Q}(\sqrt {f(r)})$ for $r \in {\mathcal F}(N)$ .

Similarly, define the set ${\mathcal Q}_f(N)$ of discriminants of the quadratic fields ${\mathbb Q}\sqrt {f(n)})$ for $n\in \{1, \ldots , N\}$ . For linear and quadratic polynomials f, Cutter et al. [5, Theorems 1A and 1B] gave an asymptotic formula for $\# {\mathcal Q}_f(N)$ . In the case of quadratic polynomials, Luca and Shparlinski [11, Theorem 2] improved the saving in the error term of [5, Theorem 1B] from $\log N$ to $N^{-1/3}$ . For polynomials f of higher degree $d \ge 3$ , an asymptotic formula for $\# {\mathcal Q}_f(N)$ is only known conditionally under the $ABC$ -conjecture (see [5, Theorem 1C]). Several additional results on the distribution of the fields ${\mathbb Q}(\sqrt {f(n)})$ for $n\in \{1, \ldots , N\}$ have been given in [12].

Kulkarni and Levin [10] initiated the study of the distribution of the fields ${\mathbb Q}(\sqrt {f(r)})$ for $r \in {\mathcal F}(N)$ . In particular, by a special case of [10, Theorem 1.2],

(1.1) $$ \begin{align} \# {\mathcal R}_f(N) \ge c(f) \frac{N^2} {(\log N)^2}, \end{align} $$

with some constant $c(f)> 0$ depending only on f. To show (1.1), Kulkarni and Levin [10] used a slightly modified result of Stewart and Top [15, Theorem 2] on squarefree parts of binary forms.

Here we use a different approach similar to that of [12] to obtain some results about the statistics of individual values of discriminants of the fields ${\mathbb Q}(\sqrt {f(r)})$ for $r \in {\mathcal F}(N)$ . More precisely, our approach is based on the square-sieve of Heath-Brown [7] combined with various bounds on double character sums.

1.2 General conventions

We use the Landau symbols ‘O’ and ‘o’ as well as the Vinogradov symbols ‘ $\gg $ ’ and ‘ $\ll $ ’ with their usual meanings. We recall that $A = O(B)$ , $A \ll B$ and $B \gg A$ are all equivalent to the inequality $|A| \le c B$ with some constant $c> 0$ , while $A=o(B)$ means that $A/B$ tends to zero. The implied constants in ‘O’, ‘ $\ll $ ’ and ‘ $\gg $ ’ may depend on the polynomial $f(X)$ .

For a real $A\ge 1$ , we write $a \sim A$ to indicate that $A \le a \le 2A$ .

1.3 Our results

Given a squarefree integer $s\ge 1$ and an arbitrary integer $N \ge 1$ , we let

$$ \begin{align*} R_f(s, N)=\#\{r\in {\mathcal F}(N):~{\mathbb Q}(\sqrt{f(r)}) = {\mathbb Q}(\sqrt{s})\}. \end{align*} $$

For a similar quantity

$$ \begin{align*} Q_f(s, N)=\#\{n\in \{1, \ldots, N\}:~{\mathbb Q}(\sqrt{f(n)}) = {\mathbb Q}(\sqrt{s})\}, \end{align*} $$

the upper bound

$$ \begin{align*} Q_f(s, N) \ll N^{1/2} \log N \end{align*} $$

is given in [12, Theorem 1.1] and a similar argument can easily yield

$$ \begin{align*} R_f(s, N) \ll N^{3/2} \log N. \end{align*} $$

However, here we take advantage of having essentially a two-dimensional problem and thus we can get savings from each variable (the numerator and denominator of $r \in {\mathcal F}(N)$ ). Hence, we obtain a stronger bound.

Theorem 1.1. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. Then uniformly over squarefree integers $s\ge 1$ and for any integer $N \ge 2$ ,

$$ \begin{align*} R_f(s, N) \ll N^{4/3} (\log N)^{4/3}. \end{align*} $$

We also show that on average over $s \in \{1, \ldots , S\}$ , a better bound can be obtained provided that S is in a certain specific region with respect to N. More precisely, let us define

$$ \begin{align*} T_f(S, N) = \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S} R_f(s, N). \end{align*} $$

Clearly, from Theorem 1.1 and also from the trivial bound,

(1.2) $$ \begin{align} T_f(S, N) \ll \min\{N^{4/3} S (\log N)^{4/3} , N^2\}. \end{align} $$

Similarly, we note that the argument of the proof of [12, Theorem 1.3] immediately implies

(1.3) $$ \begin{align} T_f(S, N) \ll N^{3/2+o(1)} S^{3/4}. \end{align} $$

We now obtain a bound which improves (1.2) and (1.3) for $S \le N^{4/5}.$

Theorem 1.2. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. Then uniformly for $S\ge 1$ ,

$$ \begin{align*} T_f(S,N) \le N^{4/3+ o(1)} S^{5/6}, \quad\mbox{as } N \to \infty.\end{align*} $$

In particular, we see from Theorem 1.2 that for all but $o(N^2)$ elements $r \in {\mathcal F}(N)$ , the field ${\mathbb Q}(\sqrt {f(r)})$ is of discriminant at least $N^{4/5+o(1)}$ .

2 Preparations

2.1 Preliminary discussion

In [10], as in [5, 11, 12], we observe that studying the fields ${\mathbb Q}(\sqrt {f(r)})$ for $r \in {\mathcal F}(N)$ is equivalent to studying the squarefree parts of $f(r)$ . To be more precise, for a rational number $\rho \ne 0$ , we define the squarefree part $S(\rho )$ as the smallest positive integer $s= S(\rho )$ such that $\rho $ can be written as

$$ \begin{align*} \rho = \pm s a^2/b^2 \end{align*} $$

with some integers a and b (it is also convenient to set $S(0) =1$ ). In particular, $S(f(r))$ is the discriminant of ${\mathbb Q}(\sqrt {f(r)})$ and thus

$$ \begin{align*} R_f(s, N)= \#\{r\in {\mathcal F}(N):~ S(f(r)) = s\}. \end{align*} $$

Next, since we are interested in upper bounds, it is convenient to discard the condition $\gcd (a,b)=1$ . In the definition of $R_f(s, N)$ , we let r run through $N^2$ (not necessarily distinct) integer ratios $a/b$ with $1\le a,b \le N$ . Hence, we work with

$$ \begin{align*} R_f^*(s, N)= \#\{(a,b) \in \{1, \ldots, N\}^2:~ S(f(a/b)) = s\} \end{align*} $$

and thus with

$$ \begin{align*} T_f^*(s, N) = \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S} R_f^*(s, N). \end{align*} $$

Finally, considering the discriminant of f, we note that if $f(X) \in {\mathbb Z}[X]$ has only simple roots, then for a sufficiently large p (depending on f), it also has only simple roots modulo p. Everywhere below, we assume that our primes are large enough to have this property.

2.2 Character sums modulo primes

Our proofs rest on some bounds for character sums. For an odd integer m, we use

$$ \begin{align*} \bigg(\frac{k}{m}\bigg), \quad k,m\in{\mathbb Z}; \ m \ge 1, \text{odd}, \end{align*} $$

to denote, as usual, the Jacobi symbol of k modulo m. Furthermore, when we write

$$ \begin{align*} \bigg(\frac{f(a/b)}{m}\bigg), \quad a,b \in{\mathbb Z}; \ m \ge 1, \text{odd}, \end{align*} $$

the value $f(a/b)$ is computed modulo m and, in particular, $\gcd (b/\gcd (a,b),m)=1$ .

We also denote

$$ \begin{align*} \mathbf{e}_m(z) = \exp(2\pi i z/m). \end{align*} $$

Lemma 2.1. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. For all primes $ p$ and all integers $\lambda $ and $\mu $ with

(2.1) $$ \begin{align} \gcd(\lambda, \mu, p) = 1, \end{align} $$

we have

$$ \begin{align*} \sum_{a = 1}^{p} \sum_{b= 1}^{p-1} \bigg(\frac{f(a/b)}{p}\bigg) \mathbf{e}_p(\lambda a + \mu b) \ll p. \end{align*} $$

Proof. Let W be the desired sum. Making the change of variable $a \mapsto ab$ (which for every fixed b runs through the full residue system modulo p together with a) and then adding the value $b=0$ to the sum, we obtain

$$ \begin{align*} W & = \sum_{a = 1}^{p} \sum_{b= 1}^{p-1} \bigg(\frac{f(a)}{p}\bigg) \mathbf{e}_p(\lambda a b + \mu b) \\ & = \sum_{a = 1}^{p} \bigg(\frac{f(a)}{p}\bigg) \sum_{b= 1}^{p} \mathbf{e}_p((\lambda a + \mu) b) + O(p). \end{align*} $$

The sum over b vanishes unless $\lambda a + \mu \equiv 0\pmod p$ , which by (2.1) is possible for only one value of a modulo p. Hence, $W = O(p)$ .

We also recall the classical Weil bound for pure character sums (see [9, Theorem 11.23]).

Lemma 2.2. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ , having only simple roots. For all primes p,

$$ \begin{align*} \sum_{a= 1}^{p} \bigg(\frac{f(a)}{p}\bigg) \ll p^{1/2}. \end{align*} $$

Lemma 2.2 immediately implies the following corollary.

Corollary 2.3. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. For all primes p,

$$ \begin{align*} \sum_{a = 1}^{p} \sum_{b= 1}^{p-1} \bigg(\frac{f(a/b)}{p}\bigg) \ll p^{3/2}. \end{align*} $$

2.3 Character sums modulo products of two primes

The following result is a direct implication of the Chinese remainder theorem for character sums (see [9, (12.20) and (12.21)]) combined with Lemma 2.1 and Corollary 2.3.

Lemma 2.4. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. Let $m = \ell p$ for two distinct primes $\ell , p \sim z$ for some real $z\ge 1$ . We have

$$ \begin{align*} \sum_{a = 1}^{m} \sum_{\substack{b= 1\\\gcd(b,m)=1} }^{m} \bigg(\frac{f(a/b)}{m}\bigg) \mathbf{e}_m(\lambda a + \mu b) \ll \begin{cases} z^{3} & \text{if}\ \gcd(\lambda, \mu, m) = m,\\ z^{5/2} & \text{if}\ 1 < \gcd(\lambda, \mu, m) < m,\\ z^{2} & \text{if}\ \gcd(\lambda, \mu, m) = 1. \end{cases} \end{align*} $$

Using the standard reduction between complete and incomplete sums (see [9, Section 12.2]), we obtain the following result.

Lemma 2.5. Let $f(X) \in {\mathbb Z}[X]$ be a fixed polynomial of degree $d \ge 2$ having only simple roots. Let $m = \ell p$ for two distinct primes $\ell , p \sim z$ for some real $z\ge 1$ . For any integers $m \ge N\ge 1$ ,

$$ \begin{align*} \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,m)=1} }^{N} \bigg(\frac{f(a/b)}{m}\bigg) \ll N^2z^{-1} + z^2 (\log z)^2. \end{align*} $$

Proof. We use the well-known bound (see, for example, [9, Bound (8.6)])

$$ \begin{align*} \sum_{a= 1}^{N} \mathbf{e}_m(\lambda z) \ll \frac{m}{|\lambda|+1}, \end{align*} $$

which holds for any integers $\lambda $ with $|\lambda | \le m/2$ and $N \le m$ . As in [9, Lemma 12.1],

(2.2) $$ \begin{align} \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,m)=1} }^{N} \bigg(\frac{f(a/b)}{m}\bigg) - \frac{N^2}{m^2} \sum_{a = 1}^{m} \sum_{\substack{b= 1\\\gcd(b,m)=1} }^{m} \bigg(\frac{f(a/b)}{m}\bigg) \ll E, \end{align} $$

where

$$ \begin{align*} E = \sum_{\substack{\lambda, \mu =0\\ (\lambda, \mu) \ne (0,0)}}^{m-1} \frac{1}{(|\lambda|+1)(|\mu|+1)} \bigg| \sum_{a = 1}^{m} \sum_{\substack{b= 1\\\gcd(b,m)=1} }^{m} \bigg(\frac{f(a/b)}{m}\bigg) \mathbf{e}_m(\lambda a + \mu b)\bigg|. \end{align*} $$

Recalling Lemma 2.4, we see that the contribution $E_1$ to E from the pairs $(\lambda , \mu )$ with $\gcd (\lambda , \mu , m) =1$ can be estimated as

$$ \begin{align*} E_1 \ll z^2 \sum_{\substack{\lambda, \mu =0\\ (\lambda, \mu) \ne (0,0)}}^{m-1} \frac{1}{(|\lambda|+1)(|\mu|+1)} \ll z^2 (\log m)^2 \ll z^2 (\log z)^2. \end{align*} $$

Next, by Lemma 2.4, we estimate the contribution $E_2$ to E from the pairs $(\lambda , \mu )$ with $1 < \gcd (\lambda , \mu , m) < m$ as

$$ \begin{align*} E_2 \ll z^{5/2} \sum_{\substack{\lambda, \mu =0\\ 1 < \gcd(\lambda, \mu, m) < m}}^{m-1} \frac{1}{(|\lambda|+1)(|\mu|+1)}. \end{align*} $$

Since $\ell $ and p are of the same size and due to the symmetry between $\lambda $ and $\mu $ , it is enough to estimate

$$ \begin{align*} \widetilde E_2 = z^{5/2} \sum_{\substack{ \lambda =0\\ p \mid \lambda}}^{m-1} \sum_{\substack{ \mu =1\\ p \mid \mu}}^{m-1} \frac{1}{(|\lambda|+1)(|\mu|+1)} = z^{5/2} \sum_{\substack{ \lambda =0\\ p \mid \lambda}}^{m-1} \frac{1}{|\lambda|+1} \sum_{\substack{ \mu =1\\ p \mid \mu}}^{m-1} \frac{1}{ |\mu|+1}. \end{align*} $$

Handling the sum over $\lambda $ in a very crude way and discarding the condition $p \mid \lambda $ ,

$$ \begin{align*} \widetilde E_2 & \le z^{5/2} \sum_{ \lambda =0}^{m-1} \frac{1}{|\lambda|+1} \sum_{\substack{ \mu =1\\ p \mid \mu}}^{m-1} \frac{1}{ |\mu|+1} \ll z^{5/2} (\log m) \sum_{\substack{ \mu =1\\ p \mid \mu }}^m \frac{1}{|\mu|+1} \\ & = z^{5/2} (\log m) \sum_{\eta =1}^\ell \frac{1}{|\eta p| +1} \ \ll z^{3/2} (\log z)^2. \end{align*} $$

Hence,

$$ \begin{align*} E_2 \ll z^{3/2} (\log z)^2, \end{align*} $$

which is dominated by the contribution from $E_1$ and we obtain

$$ \begin{align*} E \ll z^2 (\log z)^2. \end{align*} $$

Substituting this bound in (2.2) and using Lemma 2.4 again (this time in the case $\gcd (\lambda , \mu , m) =m$ ), we conclude the proof.

2.4 Large sieve inequality for Jacobi symbols

We also make use of the following bound of character sums ‘on average’ over odd squarefree moduli, which is due to Heath-Brown [8, Theorem 1].

Lemma 2.6. For all real positive numbers U and Z such that $UZ\to \infty $ and complex-valued functions $\psi (s)$ ,

$$ \begin{align*} \sum_{\substack{m \le Z\\ m~\mathrm{odd~squarefree}}} \bigg| \sum_{\substack{s \le U\\ s~\mathrm{squarefree}}} \psi(s) \bigg(\frac{s}{m}\bigg)\bigg|^2 \le (UZ)^{o(1)}(U+Z) \sum_{1 \le s \le U} |\psi(s)|^2. \end{align*} $$

3 Proofs of the main results

3.1 Proof of Theorem 1.1

Let us fix some sufficiently large real $z> 1$ and let ${\mathcal L}_z$ be the set of primes $\ell \sim z$ . By the prime number theorem,

$$ \begin{align*} \frac{z}{\log z} \ll \# {\mathcal L}_z \ll \frac{z}{\log z}. \end{align*} $$

For a rational number r, we consider the sum

$$ \begin{align*} U(r,z) =\sideset{}{^*} \sum_{\ell \in {\mathcal L}_z} \bigg(\frac{r}{\ell}\bigg), \end{align*} $$

where, as before, r is computed modulo $\ell $ and $\Sigma ^*$ means that the primes $\ell $ dividing the denominator of r are excluded.

If $r= a/b $ is a perfect square in ${\mathbb Q}$ , that is, $\sqrt {r} \in {\mathbb Q}$ , then

$$ \begin{align*} U(r,z) = \# {\mathcal L}_z +O(\log h), \end{align*} $$

where $h = \max \{|a|, |b|\} +1 $ and the term $O(\log h)$ accounts for $\ell \mid ab$ . For each $r \in Q$ with $S(f(r)) = s$ , we see that $sf(r)$ is a perfect square. Thus, for such $r \in {\mathcal F}(N)$ ,

$$ \begin{align*} U(sf(r), z) = \# {\mathcal L}_z + O(\log N) \ge \tfrac{1}{2} \# {\mathcal L}_z , \end{align*} $$

provided that

(3.1) $$ \begin{align} z \ge N^{1/2} \ge (\log N)^3 \end{align} $$

and N is large enough. In particular,

(3.2) $$ \begin{align} (\# {\mathcal L}_z)^2R_f^*(s, N) \le 4 \sum_{a,b=1}^N (U(sf(a/b), z) )^2. \end{align} $$

Squaring out, changing the order of summation, and separating the ‘diagonal term’ $N\#{\mathcal L}_z$ corresponding to $\ell = p$ , we see that

(3.3) $$ \begin{align} \sum_{a,b=1}^N (U(sf(a/b), z) )^2 \le N^2\#{\mathcal L}_z + \sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} } \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{sf(n)}{\ell p}\bigg). \end{align} $$

Substituting (3.3) in (3.2) yields

(3.4) $$ \begin{align} R_f^*(s, N) & \ll \frac{(\log z)^2}{z^2}\bigg(N^2 \frac{z}{\log z} + \sum_{\substack{\ell,p\in {\mathcal L}_z\\\ell \ne p} } \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{sf(n)}{\ell p}\bigg)\bigg)\nonumber\\& \ll \frac{N^2\log z}{z} + \frac{(\log z)^2}{z^2}\sum_{\substack{\ell,p\in {\mathcal L}_z \\ \ell \ne p} } \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{sf(n)}{\ell p}\bigg). \end{align} $$

Since $\ell p \ge z^2> N$ , we can apply Lemma 2.5 to the inner sum in (3.4), which yields

$$ \begin{align*} \sum_{\substack{\ell,p\in {\mathcal L}_z\\\ell \ne p}} \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{sf(n)}{\ell p}\bigg) \ll (\# {\mathcal L}_z)^2 (N^2z^{-1} + z^2 (\log z)^2), \end{align*} $$

which, after substitution in (3.4), implies

$$ \begin{align*} R_f^*(s, N) & \ll N^2z^{-1}\log z +N^2z^{-1} + z^2 (\log z)^2\\ & \ll N^2z^{-1}\log z + z^2 (\log z)^2. \end{align*} $$

Choosing $z=N^{2/3} (\log N)^{-1/3} $ (which obviously satisfies (3.1)), yields $R_f^*(s,N) \ll N^{4/3} (\log N)^{4/3}$ , which, in turn, implies the desired result.

3.2 Proof of Theorem 1.2

We follow the proof of Theorem 1.1. Using (3.2) for each squarefree $s\in \{1,\ldots ,S\}$ , we write

(3.5) $$ \begin{align} T_f^*(S, N)\ll z^{-2}(\log z)^2 \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S} \sum_{a,b=1}^N (U(sf(a/b), z) )^2. \end{align} $$

Instead of (3.3), we have

$$ \begin{align*} \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S }& \sum_{a,b=1}^N (U(sf(a/b), z) )^2 \\ & \le N^2 S\#{\mathcal L}_z + \sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} } \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S } \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{sf(n)}{\ell p}\bigg)\\ & \le N^2S\#{\mathcal L}_z +\sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} } \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S } \bigg(\frac{s}{\ell p}\bigg) \sum_{a = 1}^{N} \sum_{\substack{b= 1\\\gcd(b,\ell p)=1} }^{N} \bigg(\frac{f(n)}{\ell p}\bigg). \end{align*} $$

Applying Lemma 2.5, we obtain

(3.6) $$ \begin{align} \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S } & \sum_{a,b=1}^N (U(sf(a/b), z) )^2\nonumber\\& \ll N^2S\#{\mathcal L}_z + (N^2z^{-1} + z^2 (\log z)^2) \sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} } \bigg|\sum_{\substack{s=1\\ s~\text{squarefree}}}^{S} \bigg(\frac{s}{\ell p}\bigg)\bigg|.\end{align} $$

We use the Cauchy inequality to derive from Lemma 2.6 that

$$ \begin{align*} \sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} }\bigg| \sum_{\substack{s=1\\ s~\text{squarefree}}}^{S} \bigg(\frac{s}{\ell p}\bigg)\bigg| &\ll \bigg((\#{\mathcal L}_z)^2 \sum_{\substack{\ell, p\in {\mathcal L}_z\\\ell \ne p} } \bigg| \sum_{\substack{s=1\\ s~\text{squarefree}}}^{S} \bigg(\frac{s}{\ell p}\bigg)\bigg|^2\bigg)^{1/2} \\ &\ll ( (S +z^2) S^{1+ o(1)}z^{2+o(1)})^{1/2} \\ &\ll S^{1+ o(1)}z^{1+o(1)} + S^{1/2+ o(1)} z^{2+o(1)}, \end{align*} $$

as $z,S \to \infty $ . After substitution in (3.6), the last inequality yields

$$ \begin{align*} \sum_{\substack{s= 1\\ s~\text{squarefree}}}^{S } & \sum_{a,b=1}^N (U(sf(a/b), z) )^2 \\ & \ll N^2S\#{\mathcal L}_z + (N^2z^{-1} + z^2 (\log z)^2) (S^{1+ o(1)}z^{1+o(1)} + S^{1/2+ o(1)} z^{2+o(1)})\\ & \ll N^2 S^{1+ o(1)}z^{1+o(1)} + S^{1+ o(1)} z^{3+o(1)} + S^{1/2+ o(1)} z^{4+o(1)}, \end{align*} $$

as $z, S \to \infty $ (note that all terms containing N get absorbed in $N^2 S^{1+ o(1)}z^{1+o(1)}$ ). Substituting the last inequality in (3.5) gives

$$ \begin{align*} T_f^*(S,N)\ll N^2 S^{1+ o(1)}z^{-1+o(1)} + S^{1+o(1)}z^{1+o(1)} + S^{1/2+ o(1)} z^{2+o(1)}, \end{align*} $$

as $z, S \to \infty $ . We now take $z = N^{2/3} S^{1/6}$ to balance the first and the third terms (for which (3.1) is obviously satisfied). This yields

(3.7) $$ \begin{align} T_f^*(S,N)\ll N^{4/3+ o(1)} S^{5/6} + N^{2/3+o(1)} S^{7/6} \end{align} $$

(since we can always assume that $S = N^{O(1)}$ ).

We remark that by (1.2), the bound is trivial unless $N^{4/3+ o(1)} S^{5/6} \le N^2$ or $S \le N^{4/5}$ . However, under this condition, the last term in (3.7) can be dropped, which concludes the proof.