Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-16T02:46:47.520Z Has data issue: false hasContentIssue false
  • English
  • Français

ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES

Part of: Polynomials and matrices Algebraic number theory: global fields

Published online by Cambridge University Press:  05 July 2017

FLORIAN LUCA Open the ORCID record for FLORIAN LUCA [Opens in a new window]
FLORIAN LUCA*
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag X3, Wits 2050, South Africa Max Planck Institute for Mathematics, Vivatgasse 7, 53111 Bonn, Germany Department of Mathematics, Faculty of Sciences, University of Ostrava, 30. dubna 22, 701 03 Ostrava 1, Czech Republic email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We classify all polynomials 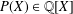$P(X)\in \mathbb{Q}[X]$ with rational coefficients having the property that the quotient 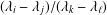$(\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{j})/(\unicode[STIX]{x1D706}_{k}-\unicode[STIX]{x1D706}_{\ell })$ is a rational number for all quadruples of roots 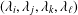$(\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D706}_{k},\unicode[STIX]{x1D706}_{\ell })$ with 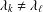$\unicode[STIX]{x1D706}_{k}\neq \unicode[STIX]{x1D706}_{\ell }$.

Keywords

roots of polynomials

MSC classification

Primary: 11C08: Polynomials
Secondary: 11R04: Algebraic numbers; rings of algebraic integers 11R32: Galois theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 185 - 190
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Berry, N., Dubickas, A., Elkies, N. D., Poonen, B. and Smyth, C., ‘The conjugate dimension of algebraic numbers’, Q. J. Math. 55 (2004), 237–252.CrossRefGoogle Scholar
Habegger, P., ‘The norm of Gaussian periods’, Preprint, 2016, arXiv:1611.07287v1.CrossRefGoogle Scholar
Saxena, N., Severini, S. and Shparlinski, I. E., ‘Parameters of integral circulant graphs and periodic quantum dynamics’, Intern. J. Q. Inf. 5 (2007), 417–430.CrossRefGoogle Scholar