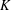Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T21:37:24.292Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PERFECT $K$-RATIONAL CUBOIDS

Part of: Arithmetic algebraic geometry Diophantine equations Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  04 October 2017

ANDREW BREMNER Open the ORCID record for ANDREW BREMNER [Opens in a new window]
ANDREW BREMNER*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe AZ 85287-1804, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 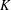$K$ be an algebraic number field. A cuboid is said to be 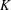$K$-rational if its edges and face diagonals lie in 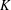$K$. A 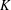$K$-rational cuboid is said to be perfect if its body diagonal lies in 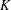$K$. The existence of perfect 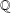$\mathbb{Q}$-rational cuboids is an unsolved problem. 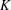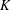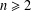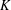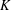We prove here that there are infinitely many distinct cubic fields $K$ such that a perfect $K$-rational cuboid exists; and that, for every integer $n\geq 2$, there is an algebraic number field $K$ of degree $n$ such that there exists a perfect $K$-rational cuboid.

Keywords

rational cuboidperfect cuboidcubic fieldRiemann–Roch

MSC classification

Primary: 11D41: Higher degree equations; Fermat's equation
Secondary: 11G05: Elliptic curves over global fields 11G35: Varieties over global fields 14G25: Global ground fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 26 - 32
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Coray, D. F., ‘Algebraic points on cubic hypersurfaces’, Acta Arith. 30 (1976), 267–296.Google Scholar
Guy, R. K., Unsolved Problems in Number Theory, 3rd edn (Springer, New York, 2004).Google Scholar
Pocklington, H. C., ‘Some Diophantine impossibilities’, Proc. Cambridge Philos. Soc. 17 (1914), 110–118.Google Scholar
Saunderson, N., The Elements of Algebra, Book 6 (Cambridge University Press, Cambridge, 1740), 429–431.Google Scholar
Spohn, W. G., ‘On the integral cuboid’, Amer. Math. Monthly 79 (1972), 57–59.Google Scholar