Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T18:12:34.775Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PAIRS OF GOLDBACH–LINNIK EQUATIONS

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  19 October 2016

YAFANG KONG  and
ZHIXIN LIU
YAFANG KONG
Affiliation:
College of Mathematics and Statistics, Chongqing Jiaotong University, Chongqing 400074, PR China email [email protected]
ZHIXIN LIU*
Affiliation:
Department of Mathematics, School of Science, Tianjin University, Tianjin 300072, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we show that every pair of large positive even integers can be represented in the form of a pair of Goldbach–Linnik equations, that is, linear equations in two primes and 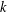$k$ powers of two. In particular, 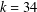$k=34$ powers of two suffice, in general, and 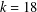$k=18$ under the generalised Riemann hypothesis. Our result sharpens the number of powers of two in previous results, which gave 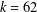$k=62$, in general, and 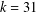$k=31$ under the generalised Riemann hypothesis.

Keywords

Goldbach–Linnik problemcircle methodpairs of equations

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes
Secondary: 11P05: Waring's problem and variants 11P55: Applications of the Hardy-Littlewood method
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 199 - 208
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11426048 and 11301372), Specialised Research Fund for the Doctoral Program of Higher Education (Grant No. 20130032120073) and Independent Innovation Foundation of Tianjin University (Grant Nos 190-0903061029 and 190-0903062072).

References

Heath-Brown, D. R. and Puchta, J. C., ‘Integers represented as a sum of primes and powers of two’, Asian J. Math. 6 (2002), 535–565.CrossRefGoogle Scholar
Kong, Y. F., ‘On pairs of linear equations in four prime variables and powers of 2’, Bull. Aust. Math. Soc. 87 (2013), 55–67.Google Scholar
Linnik, Yu. V., ‘Prime numbers and powers of two’, Tr. Mat. Inst. Steklov 38 (1951), 151–169.Google Scholar
Linnik, Yu. V., ‘Addition of prime numbers and powers of one and the same number’, Mat. Sb. (N.S.) 32 (1953), 3–60.Google Scholar
Liu, J. Y., Liu, M. C. and Wang, T. Z., ‘On the almost Goldbach problem of Linnik’, J. Théor. Nombres Bordeaux 11 (1999), 133–147.Google Scholar
Liu, Z. X. and Lü, G. S., ‘Density of two squares of primes and powers of 2’, Int. J. Number Theory 7(5) (2011), 1317–1329.Google Scholar
Platt, D. J. and Trudgian, T. S., ‘Linnik’s approximation to Goldbach’s conjecture, and other problems’, J. Number Theory 153 (2015), 54–62.CrossRefGoogle Scholar
Wrench, J. W. Jr, ‘Evaluation of Artin’s constant and the twin-prime constant’, Math. Comp. 15 (1961), 396–398.Google Scholar
Wu, J., ‘Chen’s double sieve, Goldbach’s conjecture and the twin prime problem’, Acta Arith. 114(3) (2004), 215–273.Google Scholar