Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T05:43:08.480Z Has data issue: false hasContentIssue false
  • English
  • Français

On orders of directly indecomposable finite rings

Published online by Cambridge University Press:  17 April 2009

Yasuyuki Hirano  and
Takao Sumiyama
Yasuyuki Hirano
Affiliation:
Department of Mathematics, Okayama University, Okayama 700, Japan
Takao Sumiyama
Affiliation:
Department of Mathematics, Aichi Institute of Technology, Yasuka-chô, Toyota, 470–03, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a directly indecomposable finite ring. Let p be a prime, let m be a positive integer and suppose the radical of R has pm elements. Then we show that 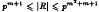. As a consequence, we have that, for a given finite nilpotent ring N, there are up to isomorphism only finitely many finite rings not having simple ring direct summands, with radical isomorphic to N. Let R* denote the group of units of R. Then we prove that (1 − 1/p)m+1 ≤ |R*| / |R| ≤ 1 − 1/pm. As a corollary, we obtain that if R is a directly indecomposable non-simple finite 2′-ring then |R| < |R*| |Rad(R)|.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 353 - 359
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Farahat, H.K., ‘The multiplicative groups of a ring’, Math. Z. 87 (1965), 378–384.CrossRefGoogle Scholar
[2]Flanigan, F.J., ‘Radical behavior and the Wedderburn family’, Bull. Amer. Math. Soc. 79 (1973), 66–70.CrossRefGoogle Scholar
[3]Hall, M., ‘The position of the radical in an algebra’, Trans. Amer. Math. Soc. 48 (1940), 391–404.CrossRefGoogle Scholar
[4]Mainwaring, D. and Pearson, K.R., ‘Decomposability of finite rings’, J. Austral. Math. Soc. Ser. A 28 (1979), 136–138.CrossRefGoogle Scholar
[5]McDonald, B.R., Finite rings with identity (Marcel Dekker, New York, 1974).Google Scholar
[6]Raghavendran, R., ‘Finite associative rings’, Compositio Math. 21 (1969), 195–229.Google Scholar
[7]Stewart, I., ‘Finite rings with a specified group of units’, Math. Z. 126 (1972), 51–58.CrossRefGoogle Scholar