Article contents
On one-sided boundedness of normed partial sums
Published online by Cambridge University Press: 17 April 2009
Extract
This paper gives a very general sufficient condition for the existence of constants B(n), C(n) for which either 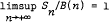 almost surely or
almost surely or 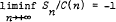 almost surely, where Sn = X1 + X2 + … + Xn and Xi are independent and identically distributed random variables. The theorem is closely connected with results of Klass and Teicher on the one-sided boundedness of Sn, with the relative stability of Sn, and with a generalised law of the iterated logarithm due to Kesten. For non negative Xi the sufficient condition is shown to be necessary, and the results are partially generalised to the case when Xi form a stationary m-dependent sequence. Some connections with a generalised type of regular variation and with domains of partial attraction are also noted.
almost surely, where Sn = X1 + X2 + … + Xn and Xi are independent and identically distributed random variables. The theorem is closely connected with results of Klass and Teicher on the one-sided boundedness of Sn, with the relative stability of Sn, and with a generalised law of the iterated logarithm due to Kesten. For non negative Xi the sufficient condition is shown to be necessary, and the results are partially generalised to the case when Xi form a stationary m-dependent sequence. Some connections with a generalised type of regular variation and with domains of partial attraction are also noted.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1980
References
- 4
- Cited by


