Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T21:26:41.715Z Has data issue: false hasContentIssue false
  • English
  • Français

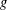ON MINIMAL ASYMPTOTIC $g$-ADIC BASES

Part of: Sequences and sets

Published online by Cambridge University Press:  05 August 2015

DENGRONG LING  and
MIN TANG
DENGRONG LING
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

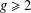Let $g\geq 2$ be a fixed integer. Let 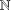$\mathbb{N}$ denote the set of all nonnegative integers and let 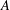$A$ be a subset of 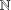$\mathbb{N}$. Write 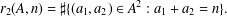$r_{2}(A,n)=\sharp \{(a_{1},a_{2})\in A^{2}:a_{1}+a_{2}=n\}.$ We construct a thin, strongly minimal, asymptotic 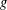$g$-adic basis 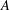$A$ of order two such that the set of $n$ with 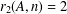$r_{2}(A,n)=2$ has density one.

Keywords

thin basisminimal asymptotic g-adic basis

MSC classification

Primary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 374 - 379
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Chen, Y. G., ‘On the Erdős–Turán conjecture’, C. R. Math. Acad. Sci. Paris 350 (2012), 933–935.CrossRefGoogle Scholar
Chen, F. J. and Chen, Y. G., ‘On minimal asymptotic bases’, European J. Combin. 32 (2011), 1329–1335.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th edn (Oxford University Press, Oxford, 1979).Google Scholar
Härtter, E., ‘Ein Beitrag zur Theorie der Minimalbasen’, J. reine angew. Math. 196 (1956), 170–204.CrossRefGoogle Scholar
Jia, X. D., ‘Minimal bases and g-adic representations of integers’, in: Number Theory (New York, 1991–1995) (Springer, New York, 1996), 201–209.CrossRefGoogle Scholar
Lee, J. B., ‘A construction of minimal asymptotic bases’, Period. Math. Hungar. 26 (1993), 211–218.CrossRefGoogle Scholar
Nathanson, M. B., ‘Minimal bases and maximal nonbases in additive number theory’, J. Number Theory 6 (1974), 324–333.CrossRefGoogle Scholar
Nathanson, M. B., ‘Minimal bases and powers of 2’, Acta Arith. 49 (1988), 525–532.CrossRefGoogle Scholar
Nathanson, M. B., ‘Cassels bases’, in: Additive Number Theory (Springer, New York, 2010), 259–285.CrossRefGoogle Scholar
Stöhr, A., ‘Gelöste und ungelöste Fragen über Basen der natürlichen Zahlenreihe II’, J. reine angew. Math. 194 (1955), 111–140.CrossRefGoogle Scholar
Tang, M., ‘On the Erdős–Turán conjecture’, J. Number Theory 150 (2015), 74–80.CrossRefGoogle Scholar
Yang, Q. H., ‘A generalization of Chen’s theorem on the Erdős–Turán conjecture’, Int. J. Number Theory 9 (2013), 1683–1686.CrossRefGoogle Scholar