Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T21:34:42.482Z Has data issue: false hasContentIssue false
  • English
  • Français

ON m-COVERS AND m-SYSTEMS

Part of: Elementary number theory Diophantine equations Sequences and sets

Published online by Cambridge University Press:  05 October 2009

ZHI-WEI SUN
ZHI-WEI SUN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 𝒜={as(mod ns)}ks=0 be a system of residue classes. With the help of cyclotomic fields we obtain a theorem which unifies several previously known results related to the covering multiplicity of 𝒜. In particular, we show that if every integer lies in more than m0=⌊∑ ks=11/ns⌋ members of 𝒜, then for any a=0,1,2,… there are at least 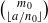subsets I of {1,…,k} with ∑ s∈I1/ns=a/n0. We also characterize when any integer lies in at most m members of 𝒜, where m is a fixed positive integer.

Keywords

covers of the integersresidue classesunit fractions

MSC classification

Secondary: 11B25: Arithmetic progressions 11A07: Congruences; primitive roots; residue systems 11B75: Other combinatorial number theory 11D68: Rational numbers as sums of fractions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 81 , Issue 2 , April 2010 , pp. 223 - 235
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2009

References

[1]Crocker, R., ‘On a sum of a prime and two powers of two’, Pacific J. Math. 36 (1971), 103–107.CrossRefGoogle Scholar
[2]Erdős, P., ‘On integers of the form 2k+p and some related problems’, Summa Brasil. Math. 2 (1950), 113–123.Google Scholar
[3]Erdős, P., ‘Remarks on number theory IV: extremal problems in number theory I’, Mat. Lapok 13 (1962), 228–255.Google Scholar
[4]Graham, R. L., Knuth, D. E. and Patashnik, O., Concrete Mathematics, 2nd edn (Addison-Wesley, Amsterdam, 1994).Google Scholar
[5]Guy, R. K., Unsolved Problems in Number Theory, 3rd edn (Springer, New York, 2004).CrossRefGoogle Scholar
[6]Koch, H., Algebraic Number Theory (Springer, Berlin, 1997).CrossRefGoogle Scholar
[7]Newman, M., ‘Roots of unity and covering sets’, Math. Ann. 191 (1971), 279–282.CrossRefGoogle Scholar
[8]Pan, H. and Zhao, L. L., ‘Clique numbers of graphs and irreducible exact m-covers of the integers’, Adv. Appl. Math. 43 (2009), 24–30.CrossRefGoogle Scholar
[9]Simpson, R. J., ‘On a conjecture of Crittenden and Vanden Eynden concerning coverings by arithmetic progressions’, J. Aust. Math. Soc. Ser. A 63 (1997), 396–420.CrossRefGoogle Scholar
[10]Sun, Z. W., ‘On exactly m times covers’, Israel J. Math. 77 (1992), 345–348.CrossRefGoogle Scholar
[11]Sun, Z. W., ‘Covering the integers by arithmetic sequences’, Acta Arith. 72 (1995), 109–129.CrossRefGoogle Scholar
[12]Sun, Z. W., ‘Covering the integers by arithmetic sequences II’, Trans. Amer. Math. Soc. 348 (1996), 4279–4320.CrossRefGoogle Scholar
[13]Sun, Z. W., ‘Exact m-covers and the linear form ∑ ks=1x s/n s’, Acta Arith. 81 (1997), 175–198.CrossRefGoogle Scholar
[14]Sun, Z. W., ‘On integers not of the form ±p a±q b’, Proc. Amer. Math. Soc. 128 (2000), 997–1002.CrossRefGoogle Scholar
[15]Sun, Z. W., ‘Algebraic approaches to periodic arithmetical maps’, J. Algebra 240 (2001), 723–743.CrossRefGoogle Scholar
[16]Sun, Z. W., ‘On the function w(x)=∣{1≤s≤k:x≡a s(mod n s)}∣’, Combinatorica 23 (2003), 681–691.CrossRefGoogle Scholar
[17]Sun, Z. W., ‘A local-global theorem on periodic maps’, J. Algebra 293 (2005), 506–512.CrossRefGoogle Scholar
[18]Sun, Z. W., ‘Finite covers of groups by cosets or subgroups’, Internat. J. Math. 17 (2006), 1047–1064.CrossRefGoogle Scholar
[19]Sun, Z. W., ‘Zero-sum problems for abelian p-groups and covers of the integers by residue classes’, Israel J. Math. 170 (2009), 235–252.CrossRefGoogle Scholar
[20]Sun, Z. W. and Yang, S. M., ‘A note on integers of the form 2n+cp’, Proc. Edinb. Math. Soc. 45 (2002), 155–160.CrossRefGoogle Scholar
[21]Wu, K. J. and Sun, Z. W., ‘Covers of the integers with odd moduli and their applications to the forms x m−2n and x 2−F 3n/2’, Math. Comp. 78 (2009), 1853–1866.CrossRefGoogle Scholar