Published online by Cambridge University Press: 23 June 2022
Let
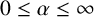 $0\leq \alpha \leq \infty $
,
$0\leq \alpha \leq \infty $
,
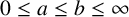 $0\leq a\leq b\leq \infty $
and
$0\leq a\leq b\leq \infty $
and
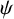 $\psi $
be a positive function defined on
$\psi $
be a positive function defined on
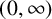 $(0,\infty )$
. This paper is concerned with the growth of
$(0,\infty )$
. This paper is concerned with the growth of
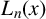 $L_{n}(x)$
, the largest digit of the first n terms in the Lüroth expansion of
$L_{n}(x)$
, the largest digit of the first n terms in the Lüroth expansion of
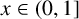 $x\in (0,1]$
. Under some suitable assumptions on the function
$x\in (0,1]$
. Under some suitable assumptions on the function
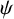 $\psi $
, we completely determine the Hausdorff dimensions of the sets
$\psi $
, we completely determine the Hausdorff dimensions of the sets
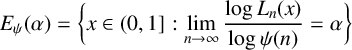 $$\begin{align*}E_\psi(\alpha)=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha\bigg\} \end{align*}$$
$$\begin{align*}E_\psi(\alpha)=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha\bigg\} \end{align*}$$
and
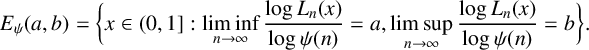 $$\begin{align*}E_\psi(a,b)=\bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=a, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=b\bigg\}. \end{align*}$$
$$\begin{align*}E_\psi(a,b)=\bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=a, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=b\bigg\}. \end{align*}$$
This research was supported by National Natural Science Foundation of China (No. 12101191), Natural Science Research Project of West Anhui University (No. WGKQ2021020) and Provincial Natural Science Research Project of Anhui Colleges (No. KJ2021A0950).