Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:35:05.014Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LITTLEWOOD–PALEY FUNCTIONS ASSOCIATED WITH THE DUNKL OPERATOR

Part of: Nontrigonometric harmonic analysis Harmonic analysis in several variables

Published online by Cambridge University Press:  29 March 2017

JIANQUAN LIAO ,
XIAOLIANG ZHANG  and
ZHONGKAI LI
JIANQUAN LIAO
Affiliation:
Department of Mathematics, Guangdong University of Education, Guangzhou, 510303, China email [email protected]
XIAOLIANG ZHANG
Affiliation:
Department of Mathematics, Capital Normal University, Beijing 100048, China email [email protected]
ZHONGKAI LI*
Affiliation:
Department of Mathematics, Shanghai Normal University, Shanghai 200234, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Littlewood–Paley operator associated with the reflection part of the Dunkl operator is introduced and proved to be of type 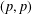$(p,p)$ for 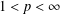$1<p<\infty$, based on boundedness of a generalised vector-valued singular integral. This fills a gap for 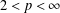$2<p<\infty$ concerning the boundedness of a 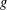$g$-function in the Dunkl setting. The paper also supplies new proofs for 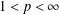$1<p<\infty$ on the 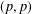$(p,p)$ boundedness of various 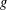$g$-functions associated with the Dunkl operator.

Keywords

Littlewood–Paley functionDunkl operator𝜆-Poisson integral𝜆-Hilbert transformDunkl transform

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 42C10: Fourier series in special orthogonal functions (Legendre polynomials, Walsh functions, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 126 - 138
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by the National Natural Science Foundation of China, Grant nos. 11326090 and 11401113, and the third author was supported by the National Natural Science Foundation of China, Grant no. 11371258.

References

Amri, B. and Sifi, M., ‘Riesz transforms for Dunkl transform’, Ann. Math. Blaise Pascal 19 (2012), 247–262.Google Scholar
Dunkl, C. F. and Xu, Y., Orthogonal Polynomials of Several Variables, 2nd edn, Encyclopedia of Mathematics and its Applications, 155 (Cambridge University Press, Cambridge, 2014).Google Scholar
Li, Zh.-K. and Liao, J.-Q., ‘Harmonic analysis associated with the one-dimensional Dunkl transform’, Constr. Approx. 37 (2013), 233–281.CrossRefGoogle Scholar
Li, Zh.-K. and Liao, J.-Q., ‘A characterization of the Hardy space $H_{\unicode[STIX]{x1D706}}^{1}(\mathbb{R})$ associated with the Dunkl transform on the line’, Math. Methods Appl. Sci., to appear.Google Scholar
Rösler, M., ‘Bessel-type signed hypergroups on ℝ’, in: Probability Measures on Groups and Related Structures XI (eds. Heyer, H. and Mukherjea, A.) (World Scientific, Singapore, 1995), 292–304.Google Scholar
Soltani, F., ‘Littlewood–Paley operators associated with the Dunkl operator on ℝ’, J. Funct. Anal. 221 (2005), 205–225.Google Scholar
Stein, E. M., ‘On the functions of Littlewood–Paley, Lusin, and Marcinkiewicz’, Trans. Amer. Math. Soc. 88 (1958), 430–466.Google Scholar
Stein, E. M., Topics in Harmonic Analysis Related to the Littlewood–Paley Theory, Annals of Mathematics Studies, 63 (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Zygmund, A., Trigonometric Series, Vols I and II, 2nd edn (Cambridge University Press, Cambridge, 1959).Google Scholar