Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T08:09:05.830Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS

Part of: Finite fields and commutative rings (number-theoretic aspects) Sequences and sets

Published online by Cambridge University Press:  30 August 2022

CESAR ANDRADE Open the ORCID record for CESAR ANDRADE [Opens in a new window] ,
YAMIDT BERMUDEZ Open the ORCID record for YAMIDT BERMUDEZ [Opens in a new window]  and
CARLOS TRUJILLO Open the ORCID record for CARLOS TRUJILLO [Opens in a new window]
CESAR ANDRADE
Affiliation:
Departamento de Matemáticas, Universidad del Valle, Cali, Colombia e-mail: [email protected]
YAMIDT BERMUDEZ*
Affiliation:
Departamento de Matemáticas, Universidad del Valle, Cali, Colombia
CARLOS TRUJILLO
Affiliation:
Departamento de Matemáticas, Universidad del Cauca, Popayan, Colombia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Sidon set is a subset of an Abelian group with the property that the sums of two distinct elements are distinct. We relate the Sidon sets constructed by Bose to affine subspaces of 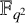$ \mathbb {F} _ {q ^ 2} $ of dimension one. We define Sidon arrays which are combinatorial objects giving a partition of the group 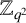$\mathbb {Z}_{q ^ 2} $ as a union of Sidon sets. We also use linear recurring sequences to quickly obtain Bose-type Sidon sets without the need to use the discrete logarithm.

Keywords

Sidon setslinear recurrencesfinite fields

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11T06: Polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 376 - 384
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bose, R. C., ‘An affine analogue of Singer’s theorem’, J. Indian Math. Soc. (N.S.) 6 (1942), 1–15.Google Scholar
Caicedo, Y., Martos, C. A. and Trujillo, C. A., ‘ $g$ -Golomb rulers’, Rev. Integr. 33 (2015), 161–172.Google Scholar
Davydov, A. A., Faina, G., Giulietti, M., Marcugini, S. and Pambianco, F., ‘On constructions and parameters of symmetric configurations ${v}_k$ ’, Des. Codes Cryptogr. 80 (2016), 125–147.CrossRefGoogle Scholar
Ganley, M. J., ‘Direct product difference sets’, J. Combin. Theory Ser. A 23 (1977), 321–332.CrossRefGoogle Scholar
Gilberto, G. P., Alberto, T. S. C. and Velasquez, J. M., ‘Construccion de conjuntos B h módulo $m$ y particiones’, Mat. E. Univ. XIV (2006), 65–70.Google Scholar
Lidl, R. and Niederreiter, H., Introduction to Finite Fields and Their Applications (Cambridge University Press, New York, 2000).Google Scholar
Lindström, B., ‘Finding finite B2-sequences faster’, Math. Comp. 67 (1998), 1173–1178.CrossRefGoogle Scholar
Martos Ojeda, C. A., Delgado Ordoñez, L. M. and Trujillo Solarte, C. A., ‘B h sets as a generalization of Golomb rulers’, IEEE Access 9 (2021), 118042–118050.CrossRefGoogle Scholar
O’Bryant, K., ‘A complete annotated bibliography of work related to Sidon sequences’, Electron. J. Combin. DS11 (2004), 39 pages.Google Scholar
Roth, R. M., Raviv, N. and Tamo, I., ‘Construction of Sidon spaces with applications to coding’, IEEE Trans. Inform. Theory 64(6) (2018), 4412–4422.CrossRefGoogle Scholar
Xiu, B., Fan, C. and Liang, M., ‘On disjoint Golomb rulers’, Preprint, 2014, arXiv:1405.4535.Google Scholar