Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-19T03:17:46.593Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 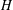$H$-ANTIMAGICNESS OF DISCONNECTED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  01 April 2016

MARTIN BAČA ,
MIRKA MILLER ,
JOE RYAN  and
ANDREA SEMANIČOVÁ-FEŇOVČÍKOVÁ
MARTIN BAČA*
Affiliation:
Department of Applied Mathematics and Informatics, Technical University, Košice, Slovakia email [email protected]
MIRKA MILLER
Affiliation:
Department of Mathematics, University of West Bohemia, Pilsen, Czech Republic School of Mathematical and Physical Sciences, The University of Newcastle, Australia email [email protected]
JOE RYAN
Affiliation:
School of Electrical Engineering and Computer Science, The University of Newcastle, Australia email [email protected]
ANDREA SEMANIČOVÁ-FEŇOVČÍKOVÁ
Affiliation:
Department of Applied Mathematics and Informatics, Technical University, Košice, Slovakia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

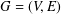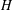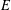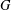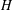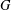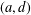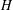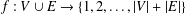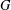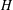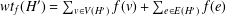A simple graph $G=(V,E)$ admits an $H$-covering if every edge in $E$ belongs to at least one subgraph of $G$ isomorphic to a given graph $H$. Then the graph $G$ is $(a,d)$-$H$-antimagic if there exists a bijection $f:V\cup E\rightarrow \{1,2,\ldots ,|V|+|E|\}$ such that, for all subgraphs $H^{\prime }$ of $G$ isomorphic to $H$, the $H^{\prime }$-weights, $wt_{f}(H^{\prime })=\sum _{v\in V(H^{\prime })}f(v)+\sum _{e\in E(H^{\prime })}f(e)$, form an arithmetic progression with the initial term $a$ and the common difference 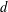$d$. When 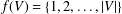$f(V)=\{1,2,\ldots ,|V|\}$, then $G$ is said to be super $(a,d)$-$H$-antimagic. In this paper, we study super $(a,d)$-$H$-antimagic labellings of a disjoint union of graphs for 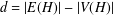$d=|E(H)|-|V(H)|$.

Keywords

H-covering(super) (a, d)-H-antimagic labellingunion of graphs

MSC classification

Primary: 05C78: Graph labelling (graceful graphs, bandwidth, etc.)
Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 201 - 207
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Arumugam, S., Miller, M., Phanalasy, O. and Ryan, J., ‘Antimagic labeling of generalized pyramid graphs’, Acta Math. Sin. (Engl. Ser.) 30(2) (2014), 283–290.Google Scholar
Bača, M., Brankovic, L. and Semaničová-Feňovčíková, A., ‘Labelings of plane graphs containing Hamilton path’, Acta Math. Sin. (Engl. Ser.) 27(4) (2011), 701–714.Google Scholar
Bača, M., Kimáková, Z., Semaničová-Feňovčíková, A. and Umar, M. A., ‘Tree-antimagicness of disconnected graphs’, Math. Probl. Eng. 2015 (2015), 504251, 4 pp., doi:10.1155/2015/504251.Google Scholar
Bača, M., Lascsáková, M., Miller, M., Ryan, J. and Semaničová-Feňovčíková, A., ‘Wheels are cycle-antimagic’, Electron. Notes Discrete Math. 48 (2015), 11–18.Google Scholar
Bača, M. and Miller, M., Super Edge-antimagic Graphs: A Wealth of Problems and Some Solutions (Brown Walker Press, Boca Raton, FL, 2008).Google Scholar
Bača, M., Miller, M., Phanalasy, O. and Semaničová-Feňovčíková, A., ‘Super d-antimagic labelings of disconnected plane graphs’, Acta Math. Sin. (Engl. Ser.) 26(12) (2010), 2283–2294.Google Scholar
Enomoto, H., Lladó, A. S., Nakamigawa, T. and Ringel, G., ‘Super edge-magic graphs’, SUT J. Math. 34 (1998), 105–109.CrossRefGoogle Scholar
Gutiérrez, A. and Lladó, A., ‘Magic coverings’, J. Combin. Math. Combin. Comput. 55 (2005), 43–56.Google Scholar
Inayah, N., Salman, A. N. M. and Simanjuntak, R., ‘On (a, d)-H-antimagic coverings of graphs’, J. Combin. Math. Combin. Comput. 71 (2009), 273–281.Google Scholar
Inayah, N., Simanjuntak, R., Salman, A. N. M. and Syuhada, K. I. A., ‘On (a, d)-H-antimagic total labelings for shackles of a connected graph H ’, Australas. J. Combin. 57 (2013), 127–138.Google Scholar
Kotzig, A. and Rosa, A., ‘Magic valuations of finite graphs’, Canad. Math. Bull. 13 (1970), 451–461.Google Scholar
Lih, K. W., ‘On magic and consecutive labelings of plane graphs’, Util. Math. 24 (1983), 165–197.Google Scholar
Lladó, A. S. and Moragas, J., ‘Cycle-magic graphs’, Discrete Math. 307 (2007), 2925–2933.Google Scholar
Marr, A. M. and Wallis, W. D., Magic Graphs (Birkhäuser, New York, 2013).Google Scholar
Maryati, T. K., Salman, A. N. M. and Baskoro, E. T., ‘Supermagic coverings of the disjoint union of graphs and amalgamations’, Discrete Math. 313 (2013), 397–405.CrossRefGoogle Scholar
Maryati, T. K., Salman, A. N. M., Baskoro, E. T., Ryan, J. and Miller, M., ‘On H-supermagic labelings for certain shackles and amalgamations of a connected graph’, Util. Math. 83 (2010), 333–342.Google Scholar
Ngurah, A. A. G., Salman, A. N. M. and Susilowati, L., ‘ H-supermagic labelings of graphs’, Discrete Math. 310 (2010), 1293–1300.CrossRefGoogle Scholar
Salman, A. N. M., Ngurah, A. A. G. and Izzati, N., ‘On (super)-edge-magic total labelings of subdivision of stars S n ’, Util. Math. 81 (2010), 275–284.Google Scholar
Simanjuntak, R., Miller, M. and Bertault, F., ‘Two new (a, d)-antimagic graph labelings’, Proc. Eleventh Australas. Workshop Combinatorial Algorithms (AWOCA) 11 (2000), 179–189.Google Scholar