ON GUILLERA’S 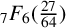${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR 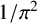${1}/{\pi ^2}$

Abstract

In 2011, Guillera [‘A new Ramanujan-like series for 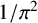$1/\pi ^2$’, Ramanujan J. 26 (2011), 369–374] introduced a remarkable rational 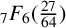${}_{7}F_{6}( \frac {27}{64} )$-series for 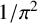${1}/{\pi ^2}$ using the Wilf–Zeilberger (WZ) method, and Chu and Zhang later proved this evaluation using an acceleration method based on Dougall’s 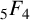${}_{5}F_{4}$-sum. Another proof of Guillera’s 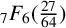${}_{7}F_{6}( \frac {27}{64} )$-series was given by Guillera in 2018, and this subsequent proof used a recursive argument involving Dougall’s sum together with the WZ method. Subsequently, Chen and Chu introduced a q-analogue of Guillera’s 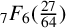${}_{7}F_{6}( \frac {27}{64} )$-series. The many past research articles concerning Guillera’s 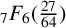${}_{7}F_{6}( \frac {27}{64} )$-series for 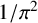${1}/{\pi ^2}$ naturally lead to questions about similar results for other mathematical constants. We apply a WZ-based acceleration method to prove new rational 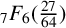${}_{7}F_{6}( \frac {27}{64} )$- and 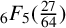${}_{6}F_{5}( \frac {27}{64} )$-series for 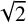$\sqrt {2}$.

1 Introduction

The study and application of the acceleration of convergence forms a major part of the discipline of numerical analysis. In this article, we offer new applications of a series acceleration method we had previously formulated in [3]. We apply this method to obtain series evaluations related to a remarkable formula due to Guillera [18].

The $\Gamma $ -function defined by $\Gamma (x) = \int _{0}^{\infty } u^{x-1} e^{-u} \, du$ for $\Re (x)> 0$ has many remarkable properties [24, Sections 17 and 20], such as the reflection formula

(1.1) $$ \begin{align} \Gamma(x) \Gamma(1-x) = \frac{\pi}{\sin(\pi x)}. \end{align} $$

The Pochhammer symbol may be defined so that $ (x)_{n} = {\Gamma (x+n)}/{\Gamma (x)}$ , and it is common to use the notation

$$ \begin{align*} \left[ \begin{matrix} \alpha, \beta, \ldots, \gamma \\ A, B, \ldots, C \end{matrix} \right]_{k} = \frac{ (\alpha)_{k} (\beta)_{k} \cdots (\gamma)_{k} }{ (A)_{k} (B)_{k} \cdots (C)_{k}}. \end{align*} $$

A generalised hypergeometric series [1] may be defined by

$$ \begin{align*} {}_{p}F_{q} \left[ \begin{matrix} a_{1}, a_{2}, \ldots, a_{p} \\ b_{1}, b_{2}, \ldots, b_{q} \end{matrix} \ \Bigg| \ x \right] = \sum_{k = 0}^{\infty} \left[ \begin{matrix} a_{1}, a_{2}, \ldots, a_{p} \\ b_{1}, b_{2}, \ldots, b_{q} \end{matrix} \right]_{k} \frac{x^{k}}{k!}. \end{align*} $$

In 2011, Guillera applied the Wilf–Zeilberger (WZ) method [23] to prove the hypergeometric formulas

(1.2) $$ \begin{align} \frac{48}{\pi^2} = \sum_{k = 0}^{\infty} \bigg( \frac{27}{64} \bigg)^{k} \left[ \begin{matrix} \frac{1}{2}, \frac{1}{2}, \frac{1}{2}, \frac{1}{3}, \frac{2}{3} \\ 1, 1, 1, 1, 1 \end{matrix} \right]_{k} ( 74 k^2 + 27 k + 3 ) \end{align} $$

and

(1.3) $$ \begin{align} \frac{16 \pi^2}{3} = \sum_{k = 0}^{\infty} \bigg( \frac{27}{64} \bigg)^{k} \left[ \begin{matrix} 1, 1, 1, \frac{5}{6}, \frac{7}{6} \\ \frac{3}{2}, \frac{3}{2}, \frac{3}{2}, \frac{3}{2}, \frac{3}{2} \end{matrix} \right]_{k} ( 74 k^2 + 101 k + 35 ). \end{align} $$

These formulas are the main sources of inspiration behind the hypergeometric formulas introduced in this article.

Subsequent to Guillera introducing (1.2) and (1.3) [18], Chu and Zhang [9], in 2014, provided alternative proofs, via an acceleration formula based on Dougall’s ${}_{5}F_{4}$ -identity, for the series of convergence rate $\frac {27}{64}$ shown in (1.2) and (1.3). Afterwards, in 2018, Guillera [19] offered yet another proof of (1.2), by applying a recursive argument using Dougall’s sum together with the WZ method. The convergence rate of $\frac {27}{64}$ of Guillera’s series in (1.2) and (1.3) was a subject of emphasis in Chen and Chu’s number-theoretic work in [4], and q-analogues of (1.2) and (1.3) were the main results of the 2021 research contribution from Chen and Chu [4]. The many research publications concerning Guillera’s formula in (1.2) [4, 9, 18, 19] motivate the development of techniques for evaluating new, high-order ${}_{p}F_{q}$ -series of convergence rate $\frac {27}{64}$ and this is the main purpose of our article.

It is easily seen that (1.2) may be expressed with a ${}_{7}F_{6}( \frac {27}{64} )$ -series. The interest in the hypergeometric formulas in (1.2) and (1.3) noted above raises the question as to how we may obtain similar results for fundamental mathematical constants apart from $\pi ^{\pm 2}$ with new rational ${}_{p}F_{q}( \frac {27}{64} )$ -series. In this article, we apply a WZ-based method we had given in [3], to prove new ${}_{7}F_{6}( \frac {27}{64} )$ - and ${}_{6}F_{5}( \frac {27}{64} )$ -series for the value $\sqrt {2}$ (sometimes referred to as Pythagoras’s constant [27]). Our new formulas for this constant closely resemble (1.2) and (1.3) and also bear a resemblance to the identities

$$ \begin{align*} \frac{105 \sqrt{2}}{4} = \sum_{k = 0}^{\infty} \bigg( \frac{-4}{27} \bigg)^{k} \left[ \begin{matrix} \frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{1}{6}, \frac{5}{6} \\ 1, \frac{11}{12}, \frac{13}{12}, \frac{17}{12}, \frac{19}{12} \end{matrix} \right]_{k} ( 1488 k^3 + 1640 k^2 + 517 k + 40 ), \end{align*} $$

$$ \begin{align*} \frac{45 \sqrt{2}}{4} = \sum_{k = 0}^{\infty} \bigg( \frac{4}{27} \bigg)^{k} \left[ \begin{matrix} \frac{1}{4}, \frac{1}{4}, \frac{3}{4}, \frac{3}{4}, \frac{3}{4} \\ 1, \frac{7}{8}, \frac{11}{8}, \frac{13}{12}, \frac{17}{12} \end{matrix} \right]_{k} ( 736 k^3 + 644 k^2 + 169 k + 12 ) \end{align*} $$

and

$$ \begin{align*} \frac{21 \sqrt{2}}{4} = \sum_{k = 0}^{\infty} \bigg( \frac{16}{27} \bigg)^{k} \left[ \begin{matrix} \frac{1}{2}, \frac{3}{4}, \frac{1}{8}, \frac{5}{8} \\ 1, \frac{5}{4}, \frac{11}{12}, \frac{19}{12} \end{matrix} \right]_{k} ( 44 k^2 + 37 k + 6 ) \end{align*} $$

given in [9]. The ${}_{4}F_{3}( {2}/{27} )$ -identity

$$ \begin{align*} \frac{3 \sqrt{2}}{4} = \sum_{k = 0}^{\infty} \bigg( \frac{2}{27} \bigg)^{k} \left[ \begin{matrix} \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \\ \frac{5}{6}, 1, \frac{7}{6} \end{matrix} \right]_{k} (5 k+1) \end{align*} $$

of Ramanujan type [6] was proved using the modified Abel lemma on summation by parts by Chu in [6] and was highlighted as a main result in [6]. This provides further motivation for the interest in Theorems 3.1 and 3.2 below.

2 Background

As in [12], the Ekhad computer system of Zeilberger produced many so-called ‘strange’ finite hypergeometric identities, through a systematised computer search for new finite summation identities for hypergeometric expressions. We have discovered experimentally that WZ pairs indicated in [12] may be applied, in conjunction with the WZ-based acceleration method from [3], to obtain new ${}_{p}F_{q}( \frac {27}{64} )$ -series resembling Guillera’s series in (1.2). It seems that our main results, which are highlighted in Theorems 3.1 and 3.2 below, are new and that there are no equivalent results given in any past literature citing [12], including [2, 5, 7, 8, 10, 11, 20, 22].

The WZ-based series acceleration method in [3] was applied, using WZ pairs corresponding to finite Catalan sum identities given by Chu and Kılıç [8], to prove new and very fast convergent series for fundamental constants such as Apéry’s constant $\zeta (3) = 1 + {1}/{2^3} + {1}/{3^3} + \cdots $ , and many of the series introduced in [3] were later included in the online reference work of the Wolfram Research company [21, 25, 26], including Campbell’s formula

(2.1) $$ \begin{align} \frac{\pi^2}{4} = \sum_{n=1}^{\infty} \frac{16^{n} (n+1) (3n+1) }{n(2n+1)^2 \binom{2n}{n}^3}, \end{align} $$

which is of convergence rate $\tfrac 14$ , and Campbell’s formula

$$ \begin{align*} -448 \zeta (3)-128 = \sum_{n=1}^{\infty} \frac{(-2^{12})^n (7168 n^5-1664 n^4-1328 n^3 + 212 n^2+49 n-9)}{n^4 (2 n-1) (3 n+1) (4 n+1) \binom{2 n}{n} \binom{3 n}{n} \binom{4 n}{2 n}^3}, \end{align*} $$

which is of convergence rate $\frac {1}{27}$ . We briefly recall some preliminaries on WZ pairs, and we briefly review the acceleration method employed in [3], which is related to WZ-based techniques given in the work of Guillera [13–19].

Bivariate hypergeometric functions $F(n, k)$ and $G(n, k)$ are said to form a WZ pair if they satisfy the discrete difference equation

(2.2) $$ \begin{align} F(n+1, k) - F(n, k) = G(n, k+1) - G(n, k), \end{align} $$

with $\lim _{k \to \infty } G(n, k) = 0$ and $G(n, 0) = 0$ [23]. We also typically work under the assumption that $F(n, k)$ , as a discrete function for integers n and k, vanishes everywhere outside a finite interval for k if n is fixed. Although WZ pairs may be thought of as having been chiefly designed for the purposes of proving conjectured evaluations for finite sums of the form $\sum _{k} F(n, k)$ by making use of the telescoping of the left-hand side of (2.2) upon the application of $\sum _{k}$ , the difference equation in (2.2) is extremely versatile in terms of identities for WZ pairs that we may derive using (2.2) and through the use of telescoping arguments. For example, Guillera has often made use of identities obtained by summing both sides of (2.2) with respect to n, as opposed to k, and Guillera’s applications of the WZ identity

(2.3) $$ \begin{align} \sum_{n=0}^{\infty} G(n, k) - \sum_{n=0}^{\infty} G(n, k+1) = F(0, k) - \lim_{n \to \infty} F(n, k) \end{align} $$

have led us to consider the following approach, as in [3].

For a WZ pair $(F, G)$ such that $\lim _{a \to \infty } F(a, r) = 0$ for all r, the WZ identity in (2.3) gives

$$ \begin{align*} -F(0, r) = \sum_{n=0}^{\infty} (G(n,r+1) - G(n,r)). \end{align*} $$

Following [3], we set the variable r to be b, and then $b+1$ , and then $b+2$ , and so forth, and then we add the resultant identities, so that a telescoping phenomenon gives

(2.4) $$ \begin{align} -\sum_{n=0}^{m} F(0, b+n) = \sum_{n=0}^{\infty} (G(n, b+m+1) - G(n, b)). \end{align} $$

We then argue, if possible (depending on possible issues concerning convergence or the interchange of limiting operations), as in [3], how the sum $ \sum _{n=0}^{\infty } G(n, b+m+1) $ may be simplified, so as to obtain an equality such as

(2.5) $$ \begin{align} -\sum_{n=0}^{\infty} F(0, b+n) = \text{constant} - \sum_{n=0}^{\infty} G(n, b). \end{align} $$

This approach was used in [3] to prove fast converging formulas as in (2.1). If both of the series in (2.5) are convergent, then (2.5) may be regarded as an acceleration formula, in view of the applications of (2.5) from [3], including the series of convergence rate $\frac {1}{27}$ for Apéry’s constant that we have reproduced above. To successfully apply (2.5) as a series acceleration identity, we need to use a WZ pair $(F, G)$ satisfying the conditions we have indicated and such that the above issues would not apply. Given a WZ pair $(F, G)$ , it seems that only in exceptional cases, (2.5) may be applied for accelerating series, which undelines the remarkable nature of Theorems 3.1 and 3.2 below.

3 New ${}_{p}F_{q}( \frac {27}{64} )$ -series

Our proof of Theorem 3.1 below involves the first WZ pair introduced in [12]. This first WZ pair corresponds to the following identity introduced in [12]:

(3.1) $$ \begin{align} {}_{2}F_{1}\!\!\left[ \begin{matrix} -n, -4n - \frac{1}{2} \\ -3n \end{matrix} \ \Bigg| \ -1 \right] = \bigg( \frac{64}{27} \bigg)^{n} \left[ \begin{matrix} \frac{3}{8}, \frac{5}{8} \\ \frac{1}{3}, \frac{2}{3} \end{matrix} \right]_{n}. \end{align} $$

Theorem 3.1. The closed-form evaluation

$$ \begin{align*} 3 \sqrt{2} = \sum _{n = 0}^{\infty} \bigg(\frac{1}{2}\bigg)^{6 n} \frac{ \big(\frac{1}{2}\big)_{3 n} \big(\frac{1}{2}\big)_{4 n} }{ \big(\frac{3}{8}\big)_n \big(\frac{1}{2}\big)_n \big(\frac{5}{8}\big)_n (1)_{4 n} } \frac{ 592 n^2-154 n+3 }{ (6 n-1) (8 n-1) } \end{align*} $$

holds.

Proof. We write the left-hand side of the Ekhad–Zeilberger identity (3.1) as a finite sum, according to the Pochhammer identity which shows that $(-n)_{k} $ vanishes for $k> n \in \mathbb {N}_{0}$ . Dividing the summand of the resultant sum by the right-hand side of (3.1), gives an expression equivalent to

$$ \begin{align*} \frac{(-1)^k \big(\frac{27}{64}\big)^n \big(\frac{1}{3}\big)_n \big(\frac{2}{3}\big)_n \big(-4 n - \frac{1}{2}\big)_k (-n)_k}{k! \big(\frac{3}{8}\big)_n \big(\frac{5}{8}\big)_n (-3 n)_k}. \end{align*} $$

To compute the above expression for noninteger values, we apply the reflection formula in (1.1) so as to obtain the hypergeometric function

$$ \begin{align*} F(n, k) = \frac{\pi 2^{-6 n} \sec \big(\frac{\pi }{8}\big) \Gamma \big(4 n+\frac{3}{2}\big) \Gamma (3 n-k+1)}{\Gamma (k+1) \Gamma \big(n+\frac{3}{8}\big) \Gamma \big(n+\frac{5}{8}\big) \Gamma (n-k+1) \Gamma \big(4 n-k+\frac{3}{2}\big)}. \end{align*} $$

So, we may apply the WZ method to obtain the WZ proof certificate given by the following verbatim output [12]:

Letting $R(n, k)$ denote the rational function given by this output, we write $ G(n, k) = R(n,k) F(n,k)$ , which shows that the WZ difference equation in (2.2) holds for the pair $(F, G)$ of bivariate mappings we have defined. Applying the summation operator $\sum _{k=0}^{m} \cdot $ to both sides of this difference equation, the left-hand side telescopes under the application of this operator, giving

$$ \begin{align*} F(m+1,k)-F(0,k) = \sum _{n=0}^m (G(n,k+1)-G(n,k)). \end{align*} $$

So,

$$ \begin{align*} -F(0, k) = \sum_{n=0}^{\infty} (G(n, k+1) - G(n, k)). \end{align*} $$

Mimicking a telescoping argument from [3], this can be used to show that (2.4) holds for the WZ pair $(F, G)$ involved in our current proof. Writing

(3.2) $$ \begin{align} \sum_{n=0}^{m} - F(0, b+n) + \sum_{n=0}^{\infty} G(n, b) = \sum_{n=0}^{\infty} G(n, b+m+1), \end{align} $$

we claim that we obtain $-\sqrt {2}$ after letting $m \to \infty $ and $b \to 0$ . It is easily seen that the left-hand side of (3.2) is convergent as $m \to \infty $ , which shows that the value of $\sum _{n=0}^{\infty } G(n, b + m + 1)$ does not depend on m. Since $G(n, 0)$ vanishes, and since

$$ \begin{align*} -F(0, 0 + n) = -\frac{\pi ^{3/2} \sec \big(\frac{\pi }{8}\big)}{2 \Gamma \big(\frac{3}{8}\big) \Gamma \big(\frac{5}{8}\big) \Gamma \big(\frac{3}{2}-n\big) \Gamma (n+1)}, \end{align*} $$

we may easily check that

$$ \begin{align*} -\sqrt{2} = \sum _{n=0}^{\infty } -F(0,0+n). \end{align*} $$

So, this gives us a proof of the identity

$$ \begin{align*} \sum _{n=0}^\infty -F(0,b+n) = -\sqrt{2}-\sum _{n=0}^{\infty} G(n,b). \end{align*} $$

Equivalently,

$$ \begin{align*} -\sqrt{2} + \frac{\sqrt{\pi }}{2 \Gamma \big(\frac{3-2 b}{2} \big) \Gamma (b+1)} \, {}_{2}F_{1}\!\!\left[ \begin{matrix} 1, b - \frac{1}{2} \\ b + 1 \end{matrix} \ \bigg| \ -1 \right] = \sum_{n=0}^{\infty} G(n, b). \end{align*} $$

Setting $b = \tfrac 12$ and applying an index shift, we obtain an equivalent formulation of the desired result.

The series highlighted in Theorem 3.1, which may be rewritten as a ${}_{6}F_{5}( \frac {27}{64} )$ - series, is very nontrivial in the sense that state-of-the-art Computer Algebra Systems are not able to provide any closed form or simplification for this high-order ${}_{p}F_{q}$ -series.

After (3.1), the next out of the forty strange identities generated by Ekhad in [12] is

(3.3) $$ \begin{align} {}_{2}F_{1}\!\!\left[ \begin{matrix} -n, -4n - \frac{5}{2} \\ -3n - 1 \end{matrix} \ \Bigg| \ -1 \right] = \bigg( \frac{64}{27} \bigg)^{n} \left[ \begin{matrix} \frac{7}{8}, \frac{9}{8} \\ \frac{2}{3}, \frac{4}{3} \end{matrix} \right]_{n}. \end{align} $$

Using the WZ certificate associated with (3.3), as given in [12], and by mimicking our proof given in Section 3, we may prove the following companion to Theorem 3.1. We may check that the series in Theorem 3.2 may be written as a ${}_{7}F_{6}( \frac {27}{64} )$ -series, giving a natural companion to Guillera’s ${}_{7}F_{6}( \frac {27}{64} )$ -series in (1.2).

Theorem 3.2. The closed-form evaluation

$$ \begin{align*} -16 \sqrt{2} = \sum _{n = 0}^{\infty} \bigg(\frac{1}{2}\bigg)^{6 n} \frac{\big(\frac{1}{2}\big)_{3 n} \big(\frac{1}{2}\big)_{4 n}}{\big(\frac{1}{8}\big)_n \big(\frac{1}{2}\big)_n \big(\frac{7}{8}\big)_n (1)_{4 n}} \frac{1184 n^3+876 n^2+216 n+29}{(2 n+1) (4 n+1) (6 n-1)} \end{align*} $$

holds.

We may obtain many similar results using variants of the finite hypergeometric identities in (3.1) and (3.3).