Hostname: page-component-66644f4456-2xp4c Total loading time: 0 Render date: 2025-02-12T13:11:29.292Z Has data issue: true hasContentIssue false
  • English
  • Français

ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS

Part of: Computational number theory Field extensions

Published online by Cambridge University Press:  10 February 2025

CHAD AWTREY Open the ORCID record for CHAD AWTREY [Opens in a new window] ,
FRANK PATANE Open the ORCID record for FRANK PATANE [Opens in a new window]  and
BRIAN TOONE Open the ORCID record for BRIAN TOONE [Opens in a new window]
CHAD AWTREY*
Affiliation:
Department of Mathematics and Computer Science, Samford University, 800 Lakeshore Drive, Birmingham, AL 35229, USA
FRANK PATANE
Affiliation:
Department of Mathematics and Computer Science, Samford University, 800 Lakeshore Drive, Birmingham, AL 35229, USA e-mail: [email protected]
BRIAN TOONE
Affiliation:
Department of Mathematics and Computer Science, Samford University, 800 Lakeshore Drive, Birmingham, AL 35229, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

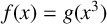Let $g(x)=x^3+ax^2+bx+c$ and $f(x)=g(x^3)$ be irreducible polynomials with rational coefficients, and let 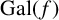$ {\mathrm{Gal}}(f)$ be the Galois group of 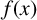$f(x)$ over 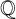$\mathbb {Q}$. We show 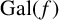$ {\mathrm{Gal}}(f)$ is one of 11 possible transitive subgroups of 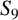$S_9$, defined up to conjugacy; we use 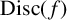$ {\mathrm{Disc}}(f)$, 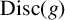$ {\mathrm{Disc}}(g)$ and two additional low-degree resolvent polynomials to identify 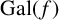$ {\mathrm{Gal}}(f)$. We further show how our method can be used for determining one-parameter families for a given group. Also included is a related algorithm that, given a field 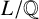$L/\mathbb {Q}$, determines when L can be defined by an irreducible polynomial of the form 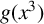$g(x^3)$ and constructs such a polynomial when it exists.

Keywords

Galois groupcomputationnonic polynomialsdiscriminant

MSC classification

Primary: 11Y40: Algebraic number theory computations
Secondary: 12F10: Separable extensions, Galois theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Awtrey, C., Beuerle, J. R. and Griesbach, H. N., ‘Field extensions defined by power compositional polynomials’, Missouri J. Math. Sci. 33(2) (2021), 163–180.CrossRefGoogle Scholar
Awtrey, C. and Jakes, P., ‘Galois groups of even sextic polynomials’, Canad. Math. Bull. 63(3) (2020), 670–676.CrossRefGoogle Scholar
Awtrey, C. and Patane, F., ‘An elementary characterization of the Galois group of a doubly even octic polynomial’, J. Algebra Appl., to appear; doi:10.1142/S0219498825502482.CrossRefGoogle Scholar
Awtrey, C., Patane, F. and Toone, B., Power Compositional Polynomial Calculator. Available from https://math.samford.edu/cubic.Google Scholar
Butler, G. and McKay, J., ‘The transitive groups of degree up to eleven’, Comm. Algebra 11(8) (1983), 863–911.CrossRefGoogle Scholar
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138 (Springer-Verlag, Berlin, 1993).CrossRefGoogle Scholar
Dixon, J. D., ‘Computing subfields in algebraic number fields’, J. Aust. Math. Soc. Ser. A 49(3) (1990), 434–448.CrossRefGoogle Scholar
Dummit, D. S. and Foote, R. M., Abstract Algebra, 3rd edn (John Wiley and Sons, Inc., Hoboken, NJ, 2004).Google Scholar
Harrington, J. and Jones, L., ‘The irreducibility of power compositional sextic polynomials and their Galois groups’, Math. Scand. 120(2) (2017), 181–194.CrossRefGoogle Scholar
Harrington, J. and Jones, L., ‘Monogenic cyclotomic compositions’, Kodai Math. J. 44(1) (2021), 115–125.CrossRefGoogle Scholar
Jones, L. and Phillips, T., ‘An infinite family of ninth degree dihedral polynomials’, Bull. Aust. Math. Soc. 97(1) (2018), 47–53.CrossRefGoogle Scholar
Kang, M.-C., ‘Cubic fields and radical extensions’, Amer. Math. Monthly 107(3) (2000), 254–256.CrossRefGoogle Scholar
Kappe, L.-C. and Warren, B., ‘An elementary test for the Galois group of a quartic polynomial’, Amer. Math. Monthly 96(2) (1989), 133–137.CrossRefGoogle Scholar
Soicher, L., The computation of Galois groups, Master’s thesis (Concordia University, Montreal, 1981).Google Scholar
Stauduhar, R. P., ‘The determination of Galois groups’, Math. Comp. 27 (1973), 981–996.CrossRefGoogle Scholar
The GAP Group , ‘GAP – Groups, Algorithms, and Programming’, Version 4.8.10, 2018. Available from http://www.gap-system.org.Google Scholar
The LMFDB Collaboration , The L-functions and modular forms database (2022). Available from https://www.lmfdb.org.Google Scholar
The PARI Group, PARI/GP – Computational Number Theory, version 2.5.3, 2013. Available from http://pari.math.u-bordeaux.fr.Google Scholar