Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T21:19:55.170Z Has data issue: false hasContentIssue false
  • English
  • Français

ON FUNCTIONS ATTRACTING POSITIVE ENTROPY

Part of: Maps and general types of spaces defined by maps Topological dynamics Real functions

Published online by Cambridge University Press:  04 October 2017

ANNA LORANTY Open the ORCID record for ANNA LORANTY [Opens in a new window]  and
RYSZARD J. PAWLAK Open the ORCID record for RYSZARD J. PAWLAK [Opens in a new window]
ANNA LORANTY*
Affiliation:
Faculty of Mathematics and Computer Science, Łódź University, Banacha 22, 90-238 Łódź, Poland email [email protected]
RYSZARD J. PAWLAK
Affiliation:
Faculty of Mathematics and Computer Science, Łódź University, Banacha 22, 90-238 Łódź, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine dynamical systems which are ‘nonchaotic’ on a big (in the sense of Lebesgue measure) set in each neighbourhood of a fixed point 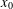$x_{0}$, that is, the entropy of this system is zero on a set for which 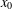$x_{0}$ is a density point. Considerations connected with this family of functions are linked with functions attracting positive entropy at 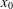$x_{0}$, that is, each mapping sufficiently close to the function has positive entropy on each neighbourhood of 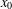$x_{0}$.

Keywords

approximately continuous function0-approximately continuous functionentropy0-approximate stable point

MSC classification

Primary: 26A18: Iteration
Secondary: 37B40: Topological entropy 54C70: Entropy 26A15: Continuity and related questions (modulus of continuity, semicontinuity, discontinuities, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 69 - 79
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Adler, R. L., Konheim, A. G. and McAndrew, M. H., ‘Topological entropy’, Trans. Amer. Math. Soc. 114(2) (1965), 309–319.CrossRefGoogle Scholar
Bartoszewicz, A., Bienias, M., Filipczak, M. and Gła̧b, Sz., ‘Strong c-algebrability of strong Sierpiński–Zygmund, smooth nowhere analytic and other sets of functions’, J. Math. Anal. Appl. 412(2) (2014), 620–630.CrossRefGoogle Scholar
Blanchard, F., ‘Topological chaos: what may this mean?’, J. Difference Equ. Appl. 15(1) (2009), 23–46.CrossRefGoogle Scholar
Bowen, R., ‘Entropy for group endomorphisms and homogeneous spaces’, Trans. Amer. Math. Soc. 153 (1971), 401–414.CrossRefGoogle Scholar
Bruckner, A. M., Differentiation of Real Functions, Lecture Notes in Mathematics, 659 (Springer, Heidelberg, 1978).CrossRefGoogle Scholar
Bruckner, A. M. and Ceder, J. G., ‘Darboux continuity’, Jahresber. Dtsch. Math.-Ver. 67 (1965), 93–117.Google Scholar
Ceder, J., ‘On Darboux points of real functions’, Period. Math. Hungar. 11(1) (1980), 69–80.CrossRefGoogle Scholar
Čiklová, M., ‘Dynamical systems generated by functions with G 𝛿 graphs’, Real Anal. Exchange 30(2) (2004), 617–638.CrossRefGoogle Scholar
Denjoy, A., ‘Sur les fonctions dérivées sommables’, Bull. Soc. Math. France 43 (1915), 161–248.CrossRefGoogle Scholar
Dinaburg, E. I., ‘Connection between various entropy characterizations of dynamical systems’, Izv. Ross. Akad. Nauk Ser. Mat. 35(2) (1971), 324–366 (in Russian).Google Scholar
Filipczak, M., Hejduk, J. and Wilczyński, W., ‘On homeomorphisms of the density type topologies’, Ann. Soc. Math. Pol. Ser. I Commentat. Math. 45(2) (2005), 151–159.Google Scholar
Kolyada, S. and Snoha, L., ‘Topological entropy of nonautonomous dynamical systems’, Random Comput. Dyn. 4 (1996), 205–233.Google Scholar
Korczak-Kubiak, E., Loranty, A. and Pawlak, R. J., ‘On focusing entropy at a point’, Taiwanese J. Math. 20(5) (2016), 1117–1137.CrossRefGoogle Scholar
Lipiński, J. S., ‘On Darboux points’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 26(11) (1978), 869–873.Google Scholar
Loranty, A. and Pawlak, R. J., ‘Stable, almost stable and odd points of dynamical systems’, Bull. Aust. Math. Soc. (to appear).Google Scholar
Luis, R., Elaydi, S. and Oliveira, H., ‘Nonautonomous periodic systems with Allee effects’, J. Difference Equ. Appl. 16 (2010), 1179–1196.CrossRefGoogle Scholar
Oxtoby, J. C., Measure and Category (Springer, New York, 1980).CrossRefGoogle Scholar
Pawlak, R. J., ‘On points of extreme chaos for almost continuous functions’, Tatra Mt. Math. Publ. 62(1) (2015), 151–164.Google Scholar
Pawlak, R. J., Korczak-Kubuak, E. and Loranty, A., ‘On some open problems connected with discrete dynamical systems in abstract analysis’, Folia Math. 19(1) (2017), 9–29.Google Scholar
Ye, X. and Zhang, G., ‘Entropy points and applications’, Trans. Amer. Math. Soc. 359(12) (2007), 6167–6186.CrossRefGoogle Scholar