ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN 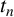$t_n$ CLASS INVARIANTS

Abstract

We study the discriminants of the minimal polynomials 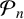$\mathcal {P}_n$ of the Ramanujan 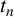$t_n$ class invariants, which are defined for positive 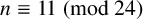$n\equiv 11\pmod {24}$. We show that 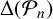$\Delta (\mathcal {P}_n)$ divides 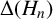$\Delta (H_n)$, where 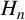$H_n$ is the ring class polynomial, with quotient a perfect square and determine the sign of 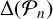$\Delta (\mathcal {P}_n)$ based on the ideal class group structure of the order of discriminant 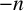$-n$. We also show that the discriminant of the number field generated by 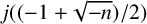$j({(-1+\sqrt {-n})}/{2})$, where j is the j-invariant, divides 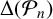$\Delta (\mathcal {P}_n)$. Moreover, using Ye’s computation of 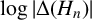$\log|\Delta(H_n)|$ [‘Revisiting the Gross–Zagier discriminant formula’, Math. Nachr. 293 (2020), 1801–1826], we show that 3 never divides 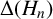$\Delta(H_n)$, and thus 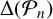$\Delta(\mathcal{P}_n)$, for all squarefree 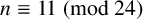$n\equiv11\pmod{24}$.

1 Introduction and main results

Let E be an elliptic curve over ${\mathbb {C}}$ that has complex multiplication (CM) by an imaginary quadratic order $\mathcal {O}$ , by which we mean that the endomorphism ring $\operatorname {\mathrm {End}}(E)$ is isomorphic to $\mathcal {O}$ . Let K denote the fraction field of $\mathcal {O}$ . The j-invariant of E is an algebraic integer whose minimal polynomial over K is the ring class polynomial  $H_n$ , where $-n$ is the discriminant of $\mathcal {O}$ . (When $\mathcal {O}$ is a maximal order, $H_n$ is often called the Hilbert class polynomial.) The ring class polynomial $H_n$ is defined by

$$ \begin{align*}H_n(x) := \prod_{j(E)\in\operatorname{\mathrm{Ell}}_{\mathcal{O}}({\mathbb{C}})}(x-j(E)),\end{align*} $$

where $\operatorname {\mathrm {Ell}}_{\mathcal {O}}({\mathbb {C}}) := \{j(E):\operatorname {\mathrm {End}}(E)\cong \mathcal {O}\}$ is the set of j-invariants of elliptic curves E over ${\mathbb {C}}$ with CM by the imaginary quadratic order $\mathcal {O}$ with discriminant $\operatorname {\mathrm {disc}}(\mathcal {O})=-n$ .

Moreover, $H_n \in {\mathbb {Z}}[x]$ and its splitting field over the imaginary quadratic field K is the ring class field $K_{\mathcal {O}}$ , which is an abelian extension of K whose Galois group $\operatorname {\mathrm {Gal}}(K_{\mathcal {O}}/K)$ is isomorphic to the class group $\operatorname {\mathrm {Cl}}(\mathcal {O})$ , via the Artin map. This is indeed a remarkable result as it implies that of uncountably many isomorphism classes of elliptic curves over ${\mathbb {C}}$ , only countably many have CM.

In his third notebook [11, pages 392–393], Ramanujan defined the values

$$ \begin{align*} t_n := \dfrac{f(\sqrt[3]{q_n})f(q_n^3)}{f^2(q_n)}\sqrt{3}q_n^{1/18}, \end{align*} $$

where $q_n=\exp (-\pi \sqrt {n})$ and $ f(-q)=\prod _{n\geqslant 1}(1-q^n).$ For all positive $n\equiv 11\pmod {24}$ , let $\mathcal {P}_n$ be the minimal polynomial of $t_n$ over ${\mathbb {Q}}$ . Without any further explanation on how he found them, Ramanujan gave the polynomials $\mathcal {P}_n$ based on $t_n$ for the first five values of $n \equiv 11\pmod {24}$ (see Table 1).

Table 1 Ramanujan’s table of $\mathcal {P}_n$ for $n=11,35,59,83,107$ .

Berndt and Chan [2, Theorem 1.2] later verified these claims, using laborious computations involving Greenhill polynomials and Weber class invariants, and proved that each $\mathcal {P}_n$ has $t_n$ as a root. Because of its computational complexity, their method could not be applied for higher values of n. However, they proved the following result.

Theorem 1.1 [2, Theorem 4.1].

Let $n \equiv 11 \pmod {24}$ be a squarefree positive integer, and suppose that the class number of the associated imaginary quadratic field ${\mathbb {Q}}(\sqrt {-n})$ is odd. Then, $t_n$ is a real unit generating the ring class field over ${\mathbb {Q}}(\sqrt {-n})$ with respect to the order of discriminant $-n$ .

Ten years later, Konstantinou and Kontogeorgis [7] generalised this result by removing the constraint that the class number be odd and also provided an efficient method for constructing the minimal polynomials $\mathcal {P}_n$ of $t_n$ over $\mathbb {Q}$ from the Ramanujan values $t_n$ for $n \equiv 11 \pmod {24}$ , using the Shimura reciprocity law. They also proved that the Ramanujan value $t_n$ is a class invariant for $n \equiv 11 \pmod {24}$ [7, Theorem 3.4]. It follows that the degree of $\mathcal {P}_n$ equals the class number of the order of discriminant $-n$ for all positive integers $n \equiv 11 \pmod {24}$ .

Let $\mathfrak {j}_n=j(({-1+\sqrt {-n})}/{2})$ , for all $n\in {\mathbb {N}}$ , where j denotes the j-invariant as defined in Section 2.1. In a follow-up paper in 2010, Konstantinou and Kontogeorgis proved the following important result.

Proposition 1.2 [8, Lemma 3].

Suppose $R_{\mathcal {P}}$ is a real root of a Ramanujan polynomial $\mathcal {P}_n$ . Then, the real number $R_H=(R_{\mathcal {P}}^6 - 27R_{\mathcal {P}}^{-6}-6)^3$ is a real root of the corresponding ring class polynomial $H_n$ .

In their proof, they show that, letting $R_{\mathcal {P}}=t_n$ gives $ \mathfrak {j}_n=(t_n^6-27t_n^{-6}-6)^3$ [8, page 12]. Moreover, notice that ${\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$ , which also follows from Section 3.1.

The coefficients of the polynomial $\mathcal {P}_n$ have remarkably smaller size compared to the coefficients of the corresponding ring class polynomial $H_n$ , suggesting that they may be useful for generating elliptic curves over prime fields by the CM method. Proposition 1.2 supports this because it shows that the roots of the polynomials $\mathcal {P}_n$ can be transformed to the roots of $H_n$ . For more details on constructing elliptic curves with the CM method, see [1, 4].

We study the discriminant of $\mathcal {P}_n$ . The historical precedent for doing so comes from [6] in which the prime factorisations of certain resultants of ring class polynomials are computed. In [6], Gross and Zagier computed the prime factorisation of the discriminant of the ring class polynomial associated to the fundamental discriminant $-p$ , where $p\equiv 3\pmod {4}$ is a prime. This result was later generalised by Dorman [5] to ring class polynomials associated to arbitrary fundamental discriminants and by Ye [14] to ring class polynomials associated to certain nonfundamental discriminants.

1.1 Notation

Fix a positive integer $n\equiv 11\pmod {24}$ and let $K={\mathbb {Q}}(\sqrt {-n})$ denote the associated imaginary quadratic field. Let $h_n$ and $\operatorname {\mathrm {Cl}}(n)$ denote the class number and ideal class group of the order of discriminant $-n$ , respectively, and let $\operatorname {\mathrm {Cl}}(n)[2]$ be the subgroup of $\operatorname {\mathrm {Cl}}(n)$ consisting of elements of order at most $2$ .

1.2 Main results

Our first main result relates $\Delta (H_n)$ to $\Delta (\mathcal {P}_n)$ .

Theorem 1.3. For all positive $n\equiv 11\pmod {24}$ ,

$$ \begin{align*} \Delta(H_n)=\Delta(\mathcal{P}_n)[{\mathbb{Z}}[t_n]:{\mathbb{Z}}[\mathfrak{j}_n]]^2, \end{align*} $$

where $[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]$ is the index of ${\mathbb {Z}}[\mathfrak {j}_n]$ in ${\mathbb {Z}}[t_n]$ .

Remark 1.4. Since the quotient $[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]^2$ is a perfect square, we deduce that $ \Delta (H_n)$ and $\Delta (\mathcal {P}_n)$ have the same sign for all positive integers $n\equiv 11\pmod {24}$ .

Let $\mathcal {D}(\mathfrak {F})$ denote the discriminant of an algebraic number field $\mathfrak {F}$ . Our next main result is the following result.

Theorem 1.5. For all positive integers $n\equiv 11\pmod {24}$ ,

$$ \begin{align*}\Delta(\mathcal{P}_n)=\mathcal{D}({\mathbb{Q}}(\mathfrak{j}_n))[\mathcal{O}_{{\mathbb{Q}}(\mathfrak{j}_n)} : {\mathbb{Z}}[t_n]]^2,\end{align*} $$

where $[\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)} : {\mathbb {Z}}[t_n]]$ is the index of ${\mathbb {Z}}[t_n]$ inside $\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$ .

Remark 1.6. Dorman explicitly computed $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$ in [5]. More precisely, he proved in [5, Proposition 5.1] that, for a squarefree positive integer $n\equiv 11\pmod {24}$ ,

(1.1) $$ \begin{align} \mathcal{D}({\mathbb{Q}}(\mathfrak{j}_n))=\pm \mathfrak{D}_0^{{h_n}/{2}}\cdot \mathfrak{D}_1^{{(h_n-2^{\mathfrak{t}-1})}/{2}}, \end{align} $$

where $\mathfrak {t}$ is the number of distinct prime factors of n and $n=\mathfrak {D}_0 \mathfrak {D}_1$ with

$$ \begin{align*}\mathfrak{D}_1=\begin{cases} 1 & \textrm{if at least } 2 \textrm{ primes congruent to } 3 \textrm{ mod } 4 \textrm{ divide } n, \\ p & \textrm{if } p \textrm{ is the unique prime congruent to } 3 \textrm{ mod } 4 \textrm{ dividing } n. \end{cases}\end{align*} $$

Note that there is a factor of $\pm 1$ in (1.1), although this factor does not appear in [5, Proposition 5.1], because Dorman computes the absolute value of $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$ .

Next, we explicitly determine the sign of $\Delta (\mathcal {P}_n)$ .

Theorem 1.7. For all positive $n\equiv 11\pmod {24}$ , $\Delta (\mathcal {P}_n)>0$ if and only if

$$ \begin{align*} h_n \equiv |\!\operatorname{\mathrm{Cl}}(n)[2]| \pmod{4}, \end{align*} $$

where $\operatorname {\mathrm {Cl}}(n)[2]$ is the subgroup of $\operatorname {\mathrm {Cl}}(n)$ consisting of elements of order at most $2$ .

Using the ambiguous class number formula from genus theory, we find that for all positive squarefree integers $n\equiv 11\pmod {24}$ ,

$$ \begin{align*} |\!\operatorname{\mathrm{Cl}}(n)[2]|=2^{\mathfrak{t}-1},\end{align*} $$

where $\mathfrak {t}$ is the number of distinct prime factors of n. Therefore, we have the following corollary.

Corollary 1.8. For all positive squarefree $n\equiv 11\pmod {24}$ , $\Delta (\mathcal {P}_n)>0$ if and only if

$$ \begin{align*}h_n\equiv2^{\mathfrak{t}-1}\pmod{4},\end{align*} $$

where, as usual, $\mathfrak {t}$ denotes the number of distinct prime factors of n.

Moreover, when the ideal class group is a cyclic group, that is $\operatorname {\mathrm {Cl}}(n)\cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$ , which is true for all $n\equiv 11\pmod {24}$ , with $11\leqslant n \leqslant 995$ as illustrated in Table 2, it is easy to see that

$$ \begin{align*}|\!\operatorname{\mathrm{Cl}}(n)[2]| =\begin{cases} 1 & \textrm{if } h_n \textrm{ is odd},\\ 2 & \textrm{if } h_n \textrm{ is even.} \end{cases}\end{align*} $$

Thus, we have the following corollary.

Table 2 Computation of the class number $h_n$ , the sign $\operatorname {\mathrm {sgn}}(\Delta )$ of $\Delta (\mathcal {P}_n)$ , the structure of the ideal class group $\operatorname {\mathrm {Cl}}(n)$ and the prime factorisation of $|\Delta (\mathcal {P}_n)|$ for all $n\equiv 11\pmod {24}$ with $11\leqslant n \leqslant 995$ .

Corollary 1.9. For all positive $n\equiv 11\pmod {24}$ , if $\operatorname {\mathrm {Cl}}(n) \cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$ , then $\Delta (\mathcal {P}_n)>0$ if and only if

$$ \begin{align*}h_n\equiv1,2\pmod{4}.\end{align*} $$

Remark 1.10. For example, two positive values of $n \equiv 11 \pmod {24}$ for which the ideal class group $\operatorname {\mathrm {Cl}}(n) \not \cong {\mathbb {Z}}/h_n{\mathbb {Z}}$ are 1235 and 2555. In particular, we find that $\operatorname {\mathrm {Cl}}(1235)\cong \operatorname {\mathrm {Cl}}(2555)\cong ({\mathbb {Z}}/6{\mathbb {Z}}) \times ({\mathbb {Z}}/2{\mathbb {Z}})$ . The structure of the ideal class group $\operatorname {\mathrm {Cl}}(n)$ for positive $n \equiv 11 \pmod {24}$ was computed using Sage [13].

In Table 2, it can be observed that 3 seems to be the only prime that never appears in the prime factorisation of $\Delta (\mathcal {P}_n)$ for positive $n \equiv 11 \pmod {24}$ . To prove this, we show that 3 never divides $\Delta (H_n)$ , and thus $\Delta (\mathcal {P}_n)$ , using Ye’s explicit computation of $\Delta (H_n)$ [14, Corollary 1.2] for squarefree positive integers $n \equiv 11 \pmod {24}$ . For more details, see Section 3.4. Therefore, we have the following important theorem.

Theorem 1.11. For all positive squarefree $n\equiv 11\pmod {24}$ , we have ${3 \nmid \Delta (\mathcal {P}_n)}$ .

1.3 Organisation of the manuscript

We start with a section on the necessary preliminaries and prove some important results that will later play a crucial role in the proofs of our main results. Proofs of Theorems 1.3, 1.5, 1.7 and 1.11 are provided in Sections 3.1, 3.2, 3.3 and 3.4, respectively. In Table 2, we have computed the class number and the ideal class group structure of ${\mathbb {Q}}(\sqrt {-n})$ , the prime factorisation and sign of $\Delta (\mathcal {P}_n)$ for all positive integers $n\equiv 11\pmod {24}$ , $11\leqslant n \leqslant 995$ , as an illustration of our main results. Finally, in Section 4, we show that all our main results hold for $n=227$ , as an example. The computations were performed using Sage [13].

2 Preliminaries: nuts and bolts

2.1 The j-invariant of a lattice

A lattice is an additive subgroup L of ${\mathbb {C}}$ which is generated by two complex numbers $\omega _1$ and $\omega _2$ that are linearly independent over ${\mathbb {R}}$ . We express this by writing $L=[\omega _1,\omega _2].$ The j-invariant $j(L)$ of a lattice L is the complex number

$$ \begin{align*} j(L)=1728\dfrac{g_2(L)^3}{g_2(L)^3-27g_3(L)^2}, \end{align*} $$

where

$$ \begin{align*} g_2(L)=60\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^4}=60\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{4}} \end{align*} $$

and

$$ \begin{align*} g_3(L)=140\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^6}=140\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{6}}, \end{align*} $$

where $L=[1,\tau ]$ with $\tau \in {\mathbb {H}}$ , the upper-half plane.

Proposition 2.1. Let L be a lattice, and let $\overline {L}$ denote the lattice obtained by complex conjugation. Then $g_2(\overline {L}) = \overline {g_2(L)}, g_3(\overline {L}) = \overline {g_3(L)}$ and $j(\overline {L}) = \overline {j(L)}$ .

Proof. From the definition of $g_2(L)$ ,

$$ \begin{align*} g_2(\overline{L})&=60\sum_{\omega\in\overline{L}\backslash\{0\}}^{}\dfrac{1}{\omega^4} =60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\overline{\omega^{4}}} =\overline{60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\omega^{4}}} =\overline{g_2(L)}. \end{align*} $$

A similar argument shows that $g_3(\overline {L}) = \overline {g_3(L)}$ and then the result for j follows from its definition.

We say that two lattices L and $L'$ are homothetic if there is a nonzero complex number $\lambda $ such that $L' = \lambda L$ . Note that homothetic lattices have the same j-invariant.

Lemma 2.2 [4, Theorem 10.9].

If L and $L'$ are lattices in ${\mathbb {C}}$ , then $j(L) = j(L')$ if and only if the lattices L and $L'$ are homothetic.

Next, we prove an important result that will later play a crucial role in the proof of Theorem 1.7.

Proposition 2.3. Let $\mathfrak {a}$ be a proper fractional $\mathcal {O}$ -ideal, where $\mathcal {O}$ is an order in an imaginary quadratic number field. Then $j(\mathfrak {a})$ is a real number if and only if the class of $\mathfrak {a}$ has order at most $2$ in the ideal class group $\operatorname {\mathrm {Cl}}(\mathcal {O})$ .

Proof. Let $\mathfrak {b}$ be the complex conjugate of the ideal $\mathfrak {a}$ . From Proposition 2.1, $j(\mathfrak {a})$ is a real number if and only if $j(\mathfrak {a})=j(\mathfrak {b})$ . Now Lemma 2.2 tells us that this is only possible when $\mathfrak {a}$ and $\mathfrak {b}$ are homothetic or, equivalently, when they represent the same ideal classes in the ideal class group $\operatorname {\mathrm {Cl}}(\mathcal {O})$ . Let $[\mathfrak {c}] \in \operatorname {\mathrm {Cl}}(\mathcal {O})$ denote the ideal class of a proper fractional $\mathcal {O}$ -ideal $\mathfrak {c}$ . Now using [4, Lemma 7.14(iii)], $[\mathfrak {b}]=[\mathfrak {a}]^{-1}$ for all $\mathfrak {a}$ . Therefore,

$$ \begin{align*} [\mathfrak{a}]=[\mathfrak{b}]\!\!\iff\!\![\mathfrak{a}]=[\mathfrak{a}]^{-1}\!\!\iff\!\![\mathfrak{a}]^2=[(1)]. \end{align*} $$

Note that this is not true as a statement about ideals; here we are explicitly referring to ideal classes, that is, elements of $\operatorname {\mathrm {Cl}}(\mathcal {O})$ .

The proposition has the following important corollary.

Corollary 2.4. The j-invariant $j(\mathcal {O})$ is a real number for any order $\mathcal {O}$ .

2.2 Discriminant of an algebraic number field

Let $\mathcal {D}(K)$ denote the discriminant of an algebraic number field K. The discriminant of a nonzero finitely generated ${\mathbb {Z}}$ -submodule $\mathfrak {M}$ of a number field K is defined as

$$ \begin{align*} \mathcal{D}(\mathfrak{M})=\mathcal{D}(\alpha_1,\alpha_2,\ldots, \alpha_n), \end{align*} $$

where $\mathfrak {M}={\mathbb {Z}}\alpha _1+{\mathbb {Z}}\alpha _2+\cdots +{\mathbb {Z}}\alpha _n$ and spans K as a ${\mathbb {Q}}$ -vector space.

Proposition 2.5 [10, Proposition 2.12].

If  $\mathfrak {M} \subset \mathfrak {M}'$ are two nonzero finitely generated ${\mathbb {Z}}$ -submodules of a number field K that span K as a ${\mathbb {Q}}$ -vector space, then the index $[\mathfrak {M}' : \mathfrak {M}]$ is finite and

$$ \begin{align*} \mathcal{D}(\mathfrak{M})=[\mathfrak{M}':\mathfrak{M}]^2 \mathcal{D}(\mathfrak{M}'). \end{align*} $$

Remark 2.6. Although Neukirch [10, Proposition 2.12] only states Proposition 2.5 for finitely generated $\mathcal {O}_K$ -submodules, the same result and proof also hold more generally for finitely generated ${\mathbb {Z}}$ -submodules.

2.3 Number fields ${\mathbb {Q}}(\mathfrak {j}_n)$ and ${\mathbb {Q}}(t_n)$

The main goal of this section is to show that the fields ${\mathbb {Q}}(\mathfrak {j}_n)$ and ${\mathbb {Q}}(t_n)$ are the same. This important result enables us to prove our main theorem, Theorem 1.5, in a very efficient way, as explained in Section 3.2.

Proposition 2.7. For all positive integers $n\equiv 11\pmod {24}$ , we have ${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$ .

Proof. To start with, consider the field diagram in Figure 1. We freely use some standard facts about the ring class fields of K throughout the proof. From class field theory, recall that if H is the ring class field associated to the discriminant of order $-n$ , then H is a finite Galois extension of K and ${[H : K] = h_n}$ , where $h_n$ denotes the class number of the order of discriminant $-n$ . Therefore, we have $[H:K]=[H:{\mathbb {Q}}(\sqrt {-n})]=h_n$ . Next, it is easy to see that $[K:{\mathbb {Q}}]=2$ since $\{1, i \sqrt {n}\}$ forms a basis. Moreover, since $H=({\mathbb {Q}}(\mathfrak {j}_n))(\sqrt {-n}),$ we have $[H : {\mathbb {Q}}(\mathfrak {j}_n)] \leqslant 2$ . Therefore, using the tower law, either $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$ or $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=2h_n$ . Now let $\mathfrak {f}$ be the minimal polynomial of $\mathfrak {j}_n \in H$ over K. Note that $\mathfrak {f}\in K[x]$ has degree $h_n$ . From Corollary 2.4, $\mathfrak {j}_n \in {\mathbb {R}}$ , that is, $\overline {\mathfrak {j}_n}=\mathfrak {j}_n$ . Thus, $\overline {\mathfrak {f}}=\mathfrak {f}$ , which implies $\mathfrak {f}\in {\mathbb {Q}}[x]$ , and we deduce that $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]\leqslant h_n$ .

Figure 1 Field diagram 1.

Putting all this together finally produces $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$ and $[H:{\mathbb {Q}}(\mathfrak {j}_n)]=2.$ Since $t_n \in {\mathbb {R}}$ , which easily follows from Ramanujan’s definition of $t_n$ , a similar argument can be applied to show that $[{\mathbb {Q}}(t_n):{\mathbb {Q}}]=h_n$ and $[H:{\mathbb {Q}}(t_n)]=2.$

The above discussion can be summarised by Figure 2.

Figure 2 Field diagram 2.

Now observe that we have the tower of fields ${\mathbb {Q}}\subseteq {\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)\subseteq H$ , where ${{\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)}$ follows from Proposition 1.2. Therefore, by the tower law,

$$ \begin{align*}[{\mathbb{Q}}(t_n):{\mathbb{Q}}(\mathfrak{j}_n)][H:{\mathbb{Q}}(t_n)]=[H:{\mathbb{Q}}(\mathfrak{j}_n)] \!\!\implies\!\![{\mathbb{Q}}(t_n):{\mathbb{Q}}(\mathfrak{j}_n)]=1,\end{align*} $$

which is only possible when ${\mathbb {Q}}(\mathfrak {j}_n) ={\mathbb {Q}}(t_n)$ . This completes the proof.

3 Proofs of the main results

3.1 Proof of Theorem 1.3

Since $t_n \in {\mathbb {Z}}[t_n]$ and the constant term of $\mathcal {P}_n$ is always $\pm 1$ (see [8, Section 3], where it is shown that $t_n$ is a unit), it follows that $t_n^{-1}\in {\mathbb {Z}}[t_n]$ . From Proposition 1.2,

$$ \begin{align*} \mathfrak{j}_n=(t_n^6-27t_n^{-6}-6)^3. \end{align*} $$

Therefore, $\mathfrak {j}_n\in {\mathbb {Z}}[t_n]$ and thus $ {\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$ . Substituting $\mathfrak {M}={\mathbb {Z}}[\mathfrak {j}_n]$ and $\mathfrak {M}'={\mathbb {Z}}[t_n]$ in Proposition 2.5 produces

$$ \begin{align*}\mathcal{D}({\mathbb{Z}}[\mathfrak{j}_n])=\mathcal{D}({\mathbb{Z}}[t_n])[{\mathbb{Z}}[t_n] : {\mathbb{Z}}[\mathfrak{j}_n]]^2\end{align*} $$

or, equivalently,

$$ \begin{align*} \Delta(H_n)=\Delta(\mathcal{P}_n)[{\mathbb{Z}}[t_n]:{\mathbb{Z}}[\mathfrak{j}_n]]^2, \end{align*} $$

which is the desired result.

3.2 Proof of Theorem 1.5

First, simply notice that

$$ \begin{align*}{\mathbb{Z}}[t_n]\subseteq\mathcal{O}_{{\mathbb{Q}}(t_n)}=\mathcal{O}_{{\mathbb{Q}}(\mathfrak{j}_n)}\subseteq{\mathbb{Q}}(\mathfrak{j}_n),\end{align*} $$

where $\mathcal {O}_{{\mathbb {Q}}(t_n)}=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$ follows from the fact that ${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$ , as shown in Proposition 2.7. As in the previous proof, substituting $\mathfrak {M}={\mathbb {Z}}[t_n]$ and $\mathfrak {M}'=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$ in Proposition 2.5 gives the desired result.

3.3 Proof of Theorem 1.7

From the definition of the ring class polynomial, its roots are

$$ \begin{align*} \{j(\mathfrak{a}) \mid \mathfrak{a}\in\operatorname{\mathrm{Cl}}(n)\}. \end{align*} $$

From Proposition 2.3, we deduce that the real roots of the ring class polynomial $H_n$ are given by

$$ \begin{align*} \{j(\mathfrak{a}) \mid \mathfrak{a}\in\operatorname{\mathrm{Cl}}(n), \textrm{order of } \mathfrak{a} \textrm{ at most } 2\}, \end{align*} $$

which is in bijection with $\operatorname {\mathrm {Cl}}(n)[2]$ .

Therefore, the number of nonreal roots of $H_n$ is given by $|\!\operatorname {\mathrm {Cl}}(n)|-|\!\operatorname {\mathrm {Cl}}(n)[2]|= h_n-|\!\operatorname {\mathrm {Cl}}(n)[2]|$ . The discriminant of a polynomial in ${\mathbb {Q}}$ is positive if and only if the number of nonreal roots of the polynomial is divisible by 4. Putting all this together completes the proof.

3.4 Proof of Theorem 1.11

Assume that n is a positive squarefree integer. Ye [14, Corollary 1.2] computed the discriminant of the ring class polynomials $H_n$ as

$$ \begin{align*} &\log|\Delta(H_n)| = \\ &-\dfrac{h_K}{4}\sum_{\substack{[\mathfrak{a}]\in\operatorname{\mathrm{Cl}}_K\\ [\mathfrak{a}]\neq[\mathcal{O}_K]}}\sum_{\ell=0}^{n-1}\sum_{X,Y=-\infty}^{\infty} \kappa\bigg(1-\dfrac{n(2AX+BY)^2+(nY-2A\ell)^2}{4An},\dfrac{B\ell}{n}f_1^{(\mathfrak{a})}-\dfrac{2A\ell}{n}f_{2}^{(\mathfrak{a})}+L_{-}^{(\mathfrak{a})}\bigg), \end{align*} $$

where $h_K$ denotes the class number of $K={\mathbb {Q}}(\sqrt {-n})$ , $L_{-}^{(\mathfrak {a})}$ denotes the lattice ${\mathbb {Z}} f_1^{(\mathfrak {a})}+{\mathbb {Z}} f_2^{(\mathfrak {a})}$ ,

$$ \begin{align*}\mathfrak{a}=\bigg[A,\dfrac{B+\sqrt{-n}}{2}\bigg], \quad f_1^{(\mathfrak{a})}=\begin{pmatrix} -1 & B \\ 0 & A \end{pmatrix}, \quad f_2^{(\mathfrak{a})}=\begin{pmatrix} 0 & C \\ 1 & 0 \end{pmatrix},\end{align*} $$

(3.1) $$ \begin{align} \kappa(m,\mu)\nonumber=&-\dfrac{1}{h_K}\sum_{q \, \textrm{inert} }^{}\xi_q(m,\mu)(\operatorname{\mathrm{ord}}_q(m)+1)\rho_K\bigg(\dfrac{mn}{q}\bigg)\log q \\ & - \dfrac{\rho_K(mn)}{h_K}\sum_{q \mid n}^{}\xi_q(m,\mu)\operatorname{\mathrm{ord}}_q(mn)\log q, \end{align} $$

and $\xi _q$ and $\rho _K$ are the functions defined in [14, Corollary 1.2].

To prove Theorem 1.11, we will show that $\log 3$ never appears in $\kappa (m,\mu )$ for any choice of parameters m and $\mu $ . From the definition of $\kappa (m,\mu )$ , it suffices to prove that 3 always splits in ${\mathbb {Q}}(\sqrt {-n})$ and does not divide n for all positive squarefree $n\equiv 11\pmod {24}$ .

Recall that a prime number $\mathfrak {p}$ splits in the imaginary quadratic field ${\mathbb {Q}}(\sqrt {-n})$ if and only if $-n$ is a nonzero quadratic residue mod $\mathfrak {p}$ . The quadratic residues mod 3 are 0 and 1, and it is easy to see that when $n\equiv 11\pmod {24}$ , we have $-n\equiv 1\pmod {3}$ . Thus $-n$ is a nonzero quadratic residue mod 3 for all positive squarefree integers $n\equiv 11\pmod {24}$ . This completes the proof.

4 An illustration of the main results

Example 4.1. Take $n=227$ . From [7, Table 1],

$$ \begin{align*}\mathcal{P}_{227}(z)=z^5-5z^4+9z^3-9z^2+9z-1.\end{align*} $$

Since 227 is squarefree, the degree of $\mathcal {P}_{227}$ is equal to the class number of ${\mathbb {Q}}(\sqrt {-227})$ ; thus, $h_{227}=5$ . The class group structure of ${\mathbb {Q}}(\sqrt {-227})$ , computed using Sage, is ${\mathbb {Z}}/5{\mathbb {Z}}$ (see Table 2). By Corollary 1.9, $\Delta (\mathcal {P}_{227})>0$ , since $h_{227}=5\equiv 1\pmod {4}.$ From Table 2, $\Delta (\mathcal {P}_{227})=2^4\cdot 227^2$ . Moreover, using the Sage database for ring class polynomials and their discriminants [13], it can be found that

$$ \begin{align*}H_{227}(z)=& \,z^5 + 360082897644683264000z^4 \\&- 2562327002832961536000000000z^3 \\&+ 18227340807938993794580480000000000z^2 \\&- 2111118203460821622718464000000000000z \\&+ 5085472193216544027705344000000000000000, \end{align*} $$

and

$$ \begin{align*}\Delta(H_{227})\!=\!2^{316}\! \cdot 5^{60}\! \cdot 13^{20}\! \cdot 17^{20} \!\cdot 31^4 \cdot 37^6 \cdot 41^4 \cdot 61^4 \cdot 83^2 {\cdot} 151^2 {\cdot} 179^2 {\cdot} 191^2 {\cdot} 199^2 {\cdot} 227^2.\end{align*} $$

Therefore,

$$ \begin{align*} \dfrac{\Delta(H_{227})}{\Delta(\mathcal{P}_{227})}&=(2^{156} \cdot 5^{30} \cdot 13^{10} \cdot 17^{10} \cdot 31^2 \cdot 37^3 \cdot 41^2 \cdot 61^2 \cdot 83 \cdot 151 \cdot 179 \cdot 191 \cdot 199)^2, \end{align*} $$

which is in accord with Theorem 1.3, since the quotient is a perfect square.

By Theorem 1.5, $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_{227}))> 0$ since $\Delta (\mathcal {P}_{227})> 0$ , as already seen above and in Table 2. From Remark 1.6, $\mathfrak {D}_0=1$ , $\mathfrak {D}_1=227$ , $\mathfrak {t}=1$ , and thus

$$ \begin{align*}\mathcal{D}({\mathbb{Q}}(\mathfrak{j}_{227}))=227^2 \mid 2^4\cdot227^2=\Delta(\mathcal{P}_{227}).\end{align*} $$

Notice that 3 does not appear in the prime factorisation of $\Delta (\mathcal {P}_{227})$ and $\Delta (H_{227})$ .

5 Concluding remarks and further research

We can now replace the ring class polynomials $H_n$ and their discriminants $\Delta (H_n)$ with the Ramanujan polynomials $\mathcal {P}_n$ and their discriminants $\Delta (\mathcal {P}_n)$ to simplify computations wherever needed. Ramanujan polynomials $\mathcal {P}_n$ can be used in the generation of special curves, such as MNT curves [9, 12], and in the generation of elliptic curves that do not necessarily have prime order [1].

Problems such as primality testing and proving [1], the generation of elliptic curve parameters [8] and the representability of primes by quadratic forms [4] could be considerably advanced once we know more about Ramanujan polynomials $\mathcal {P}_n$ and their discriminants and traces.