Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T22:34:45.867Z Has data issue: false hasContentIssue false
  • English
  • Français

ON COMMUTATIVITY OF BANACH ALGEBRAS WITH DERIVATIONS

Part of: Rings and algebras with additional structure Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  06 March 2015

SHAKIR ALI  and
ABDUL NADIM KHAN
SHAKIR ALI*
Affiliation:
Department of Mathematics, Faculty of Science, Rabigh, King Abdulaziz University, Jeddah 21589, Saudi Arabia email [email protected]
ABDUL NADIM KHAN
Affiliation:
Department of Mathematics, Aligarh Muslim University, Aligarh 202002, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

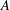The aim of this paper is to discuss the commutativity of a Banach algebra $A$ via its derivations. In particular, we prove that if 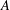$A$ is a unital prime Banach algebra and 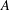$A$ has a nonzero continuous linear derivation 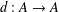$d:A\rightarrow A$ such that either 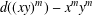$d((xy)^{m})-x^{m}y^{m}$ or 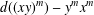$d((xy)^{m})-y^{m}x^{m}$ is in the centre of 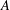$A$ for an integer 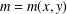$m=m(x,y)$ and sufficiently many 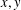$x,y$, then 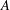$A$ is commutative. We give examples to illustrate the scope of the main results and show that the hypotheses are not superfluous.

Keywords

Banach algebraderivation

MSC classification

Primary: 16W25: Derivations, actions of Lie algebras
Secondary: 46J10: Banach algebras of continuous functions, function algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 3 , June 2015 , pp. 419 - 425
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bell, H. E., ‘On a commutativity theorem of Herstein’, Arch. Math. (Basel) 21 (1970), 265–267.CrossRefGoogle Scholar
Bell, H. E., ‘On the commutativity of prime rings with derivation’, Quaest. Math. 22(3) (1999), 329–335.Google Scholar
Bonsall, F. F. and Duncan, J., Complete Normed Algebras (Springer, New York, 1973).Google Scholar
Herstein, I. N., ‘Power maps in rings’, Michigan Math. J. 8 (1961), 29–32.CrossRefGoogle Scholar
Herstein, I. N., ‘A remark on rings and algebras’, Michigan Math. J. 10 (1963), 269–272.CrossRefGoogle Scholar
Herstein, I. N., Rings with Involution (University of Chicago Press, Chicago, 1976).Google Scholar
Hongan, M., ‘A note on semiprime rings with derivation’, Internat. J. Math. Math. Sci. 20(2) (1997), 413–415.CrossRefGoogle Scholar
Lee, P. H. and Lee, T. K., ‘Lie ideals of prime rings with derivations’, Bull. Inst. Math. Acad. Sin. (N.S.) 11(1) (1983), 75–80.Google Scholar
Mayne, J., ‘Centralizing automorphism of prime rings’, Canad. Math. Bull. 19 (1976), 113–115.Google Scholar
Posner, E. C., ‘Derivations in prime rings’, Proc. Amer. Math. Soc. 8 (1957), 1093–1100.CrossRefGoogle Scholar
Vukman, J., ‘Commuting and centralizing mappings in prime rings’, Proc. Amer. Math. Soc. 109 (1990), 47–52.CrossRefGoogle Scholar
Vukman, J., ‘A result concerning derivations in noncommutative Banach algebras’, Glas. Mat. Ser. III 26(46)(1–2) (1991), 83–88.Google Scholar
Vukman, J., ‘On derivations in prime rings and Banach algebras’, Proc. Amer. Math. Soc. 116 (1992), 877–884.Google Scholar
Yood, B., ‘Continuous homomorphisms and derivations on Banach algebras’, in: Proc. Conf. on Banach Algebras and Several Complex Variables, New Haven, CT, 1983, Contemporary Mathematics, 32 (American Mathematical Society, Providence, RI, 1984), 279–284.Google Scholar
Yood, B., ‘Commutativity theorems for Banach algebras’, Michigan Math. J. 37(2) (1990), 203–210.Google Scholar
Yood, B., ‘On commutativity of unital Banach algebras’, Bull. Lond. Math. Soc. 23(3) (1991), 278–280.Google Scholar