Article contents
On closed radical orbits in homogeneous complex manifolds
Published online by Cambridge University Press: 17 April 2009
Abstract
Suppose G is a complex Lie group having a finite number of connected components and H is a closed complex subgroup of G with H° solvable. Let RG denote the radical of G. We show the existence of closed complex subgroups I and J of G containing H such that I/H is a connected solvmanifold with I° ⊃ RG, the space G/J has a Klein form SG/A, where A is an algebraic subgroup of the semisimple complex Lie group SG: = G/RG, and, unless I = J, the space J/I has Klein form 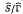 , where
, where 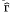 is a Zariski dense discrete subgroup of some connected positive dimensional semisimple complex Lie group Ŝ.
is a Zariski dense discrete subgroup of some connected positive dimensional semisimple complex Lie group Ŝ.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 54 , Issue 3 , December 1996 , pp. 363 - 368
- Copyright
- Copyright © Australian Mathematical Society 1996
References
- 1
- Cited by


