Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gal, Sorin G.
2013.
Overconvergence in Complex Approximation.
p.
117.
SEKİN, Çağla
GÜLOĞLU, Mutlu
and
ALİYEV, İlham
2021.
On the approximation properties of bi-parametric potential-type integral operators.
Hacettepe Journal of Mathematics and Statistics,
Vol. 50,
Issue. 6,
p.
1681.


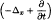 and
and 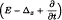 , where
, where