Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T20:31:26.407Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ADDITIVE REPRESENTATION FUNCTIONS

Part of: Sequences and sets

Published online by Cambridge University Press:  02 May 2017

YA-LI LI  and
YONG-GAO CHEN Open the ORCID record for YONG-GAO CHEN [Opens in a new window]
YA-LI LI
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210023, PR China email [email protected]
YONG-GAO CHEN*
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210023, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any finite abelian group 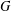$G$ with 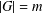$|G|=m$, 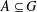$A\subseteq G$ and 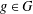$g\in G$, let 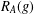$R_{A}(g)$ be the number of solutions of the equation 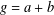$g=a+b$, 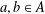$a,b\in A$. Recently, Sándor and Yang [‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Preprint, 2016, arXiv:1612.08722v1] proved that, if 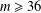$m\geq 36$ and 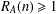$R_{A}(n)\geq 1$ for all 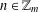$n\in \mathbb{Z}_{m}$, then there exists 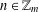$n\in \mathbb{Z}_{m}$ such that 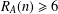$R_{A}(n)\geq 6$. In this paper, for any finite abelian group 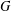$G$ with 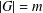$|G|=m$ and 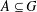$A\subseteq G$, we prove that (a) if the number of 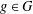$g\in G$ with 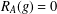$R_{A}(g)=0$ does not exceed 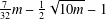$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$, then there exists 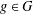$g\in G$ such that 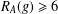$R_{A}(g)\geq 6$; (b) if 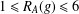$1\leq R_{A}(g)\leq 6$ for all 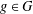$g\in G$, then the number of 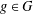$g\in G$ with 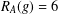$R_{A}(g)=6$ is more than 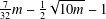$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$.

Keywords

Erdős–Turán conjectureRuzsa’s numberrepresentation functionadditive basisabelian group

MSC classification

Primary: 11B34: Representation functions
Secondary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 380 - 388
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China, Grant No. 11371195, and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

Borwein, P., Choi, S. and Chu, F., ‘An old conjecture of Erdős–Turán on additive bases’, Math. Comp. 75 (2006), 475–484.Google Scholar
Chen, Y.-G., ‘The analogue of Erdős–Turán conjecture in ℤ m ’, J. Number Theory 128 (2008), 2573–2581.Google Scholar
Chen, Y.-G., ‘On the Erdős–Turán conjecture’, C. R. Acad. Sci. Paris Sér. I 350 (2012), 933–935.Google Scholar
Chen, Y.-G. and Sun, T., ‘The difference basis and bi-basis of ℤ m ’, J. Number Theory 130 (2010), 716–726.Google Scholar
Chen, Y.-G. and Tang, M., ‘On a generalization of a theorem of Sárközy and Sós’, European J. Combin. 54 (2016), 201–206.Google Scholar
Dubickas, A., ‘A basis of finite and infinite sets with small representation function’, Electron. J. Combin. 19 (2012), #P6, 16 pages.Google Scholar
Erdős, P. and Turán, P., ‘On a problem of Sidon in additive number theory, and on some related problems’, J. Lond. Math. Soc. 16 (1941), 212–215.Google Scholar
Grekos, G., Haddad, L., Helou, C. and Pihko, J., ‘On the Erdős–Turán conjecture’, J. Number Theory 102 (2003), 339–352.Google Scholar
Konstantoulas, I., ‘Lower bounds for a conjecture of Erdős and Turán’, Acta Arith. 159 (2013), 301–313.Google Scholar
Lev, V. F. and Sárközy, A., ‘An Erdős–Fuchs type theorem for finite groups’, Integers 11 (2011), 487–494.Google Scholar
Nathanson, M. B., ‘Unique representation bases for the integers’, Acta Arith. 108 (2003), 1–8.CrossRefGoogle Scholar
Ruzsa, I. Z., ‘A just basis’, Monatsh. Math. 109 (1990), 145–151.CrossRefGoogle Scholar
Sándor, C. and Yang, Q.-H., ‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Preprint, 2016, arXiv:1612.08722v1.Google Scholar
Tang, M., ‘On the Erdős–Turán conjecture’, J. Number Theory 150 (2015), 74–80.Google Scholar
Tang, M. and Chen, Y.-G., ‘The new upper bounds of some Ruzsa numbers R m ’, J. Math. Res. Exposition 30 (2010), 557–561.Google Scholar