Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T20:46:53.817Z Has data issue: false hasContentIssue false
  • English
  • Français

On additive properties of general sequences

Published online by Cambridge University Press:  17 April 2009

Min Tang  and
Yong-Gao Chen
Min Tang
Affiliation:
Department of Mathematics, Nanjing Normal University, Nanjing 210097, China and Department of Mathematics, Anhui Normal University, Wuhu 241000, China
Yong-Gao Chen
Affiliation:
Department of Mathematics, Nanjing Normal University, Nanjing 210097, China, e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A = {a1, a2,…} (a1 < a2 < …) be an infinite sequence of positive integers. Let A(n) be the number of elements of A not exceeding n, and denote by R2(n) the number of solutions of ai + aj = n, i ≤ j. In 1986, Erdős, Sárközy and Sós proved that if (n − A(n))/log n → ∞(n → ∞), then 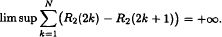. In this paper, we generalise this theorem and give its quantitative form. For example, one of our conclusions implies that if limsup(n − A(n))/log n = ∞, then 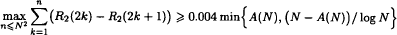for infinitely many positive integers N.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 71 , Issue 3 , June 2005 , pp. 479 - 485
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Balasubramanian, R., ‘A note on a result of Erdős, Sárközy and Sós’, Acta Arith. 49 (1987), 45–53.CrossRefGoogle Scholar
[2]Chen, Y.G. and Wang, B., ‘On additive properties of two special sequences’, Acta Arith. 110 (2003), 299–303.CrossRefGoogle Scholar
[3]Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, I’, Pacific J. Math. 118 (1985), 347–357.CrossRefGoogle Scholar
[4]Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, II’, Acta Math. Hungar. 48 (1986), 201–211.CrossRefGoogle Scholar
[5]Erdős, P., Sárközy, A. and Sós, V.T., ‘Problems and results on additive properties of general sequences, IV’, in Number theory (Ootacamund, 1984), Lecture Notes in Math. 1122 (Springer-Verlag, Berlin, 1985), pp. 85–104.CrossRefGoogle Scholar
[6]Erdős, P., Sárközy, A. and Sós, V.T., ‘Problems and results on additive properties of general sequences, V’, Monatsh. Math. 102 (1986), 183–197.CrossRefGoogle Scholar
[7]Erdős, P., Sárközy, A. and Sós, V.T., ‘Problems and results on additive properties of general sequences, III’, Studia Sci. Math. Hungar. 22 (1987), 53–63.Google Scholar
[8]Lev, V.F., ‘Reconstructing integer sets from their representation functions’, Electronic J. Combin. 11 (2004), ♯ R78.CrossRefGoogle Scholar
[9]Nathanson, M.B., ‘Representation functions of sequences in additive number theory’, Proc. Amer. Math. Soc. 72 (1978), 16–20.CrossRefGoogle Scholar