Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T18:32:24.139Z Has data issue: false hasContentIssue false
  • English
  • Français

On a theorem of Nielsen

Published online by Cambridge University Press:  17 April 2009

Saroop K. Kaul  and
Dale V. Thompson
Saroop K. Kaul
Affiliation:
Department of Mathematics, University of Regina, Regina, Saskatchewan, Canada S4S 0A2
Dale V. Thompson
Affiliation:
Department of Mathematics, Champlain Regional College, Lennexville, Quebec, Canada JOB IZO.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following theorem proved in this paper is a generalization of a result of Jakob Nielsen. Suppose G is a group of linear fractional transformations acting on the unit disc D in the complex plane; suppose also that each element of G, except the identity, is either a hyperbolic or a parabolic transformation. Then any homeomorphism h of the open disc 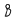onto itself which satisfies the functional equation hg = g′h, for some automorphism g → g′ of G, has a unique extension to a homeomorphism of D onto itself.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 24 , Issue 1 , August 1981 , pp. 37 - 47
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Gottschalk, Walter Helbig and Hedlund, Gustav Arnold, Topological Dynamics (American Mathematical Society Colloquium Publications, 36. American Mathematical Society, Providence, Rhode Island, 1955).Google Scholar
[2]Homma, Tatsuo and Kinoshita, Shin'ichi, “On the regularity of homeomorphisms of En”, J. Math. Soc. Japan 5 (1953), 365–371.Google Scholar
[3]Homma, Tatsuo and Kinoshita, Shin'ichi, “On homeomorphisms which are regular except for a finite number of points” Osaka Math. J. 7 (1955), 29–38.Google Scholar
[4]Kaul, S.K., “On almost regular homeomorphisms” Canad. J. Math. 20 (1968), 1–6.Google Scholar
[5]Kaul, S.K., “On a transformation group” Canad. J. Math. 21 (1969), 935–941.CrossRefGoogle Scholar
[6]Kaul, S.K., “On the irregular sets of a transformation group” Canad. Math. Bull. 16 (1973), 225–232.CrossRefGoogle Scholar
[7]von Kerékjártó, B., “Topologische Charakterisierung der linearen Abbildungen” Acta Sci. Math. (Szeged) 6 (1934), 235–262.Google Scholar
[8]Kinoshita, Shin'ichi, “Notes on a discontinuous transformation group” preprint.Google Scholar
[9]Kinoshita, Shin'ichi, “Some results and problems on covering transformation groups”, preprint.Google Scholar
[10]Kinoshita, S., “On quasi translations” 3-space topology of 3-manifolds and related topics, 223–226 (Proc. Univ. Georgia Institute, 1961. Prentice-Hall, Englewood Cliffs, New Jersey, 1962).Google Scholar
[11]Nielsen, Jakob, “Untersuchungen zur Topologie der Geschlossenen Zweiseitigen Flachen” Acta Math. 50 (1927), 189–358.CrossRefGoogle Scholar
[12]Spanier, Edwin H., Algebraic topology (McGraw-Hill, New York, Toronto, London, 1966).Google Scholar