Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T08:07:20.023Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A QUESTION OF HARTWIG AND LUH

Part of: Conditions on elements Homological methods

Published online by Cambridge University Press:  13 June 2013

SAMUEL J. DITTMER ,
DINESH KHURANA  and
PACE P. NIELSEN
SAMUEL J. DITTMER
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA email [email protected]
DINESH KHURANA
Affiliation:
Department of Mathematics, Panjab University, Chandigarh 160 014, India email [email protected]
PACE P. NIELSEN*
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602, USA
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1977 Hartwig and Luh asked whether an element $a$ in a Dedekind-finite ring 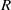$R$ satisfying 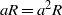$aR= {a}^{2} R$ also satisfies 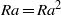$Ra= R{a}^{2} $. In this paper, we answer this question in the negative. We also prove that if $a$ is an element of a Dedekind-finite exchange ring 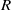$R$ and 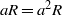$aR= {a}^{2} R$, then 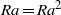$Ra= R{a}^{2} $. This gives an easier proof of Dischinger’s theorem that left strongly 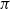$\pi $-regular rings are right strongly 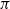$\pi $-regular, when it is already known that 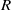$R$ is an exchange ring.

Keywords

Dedekind-finite ringsDischinger’s theoremexchange ringsstrongly π-regular rings

MSC classification

Secondary: 16E50: von Neumann regular rings and generalizations 16U99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 271 - 278
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ara, P., ‘Strongly $\pi $-regular rings have stable range one’, Proc. Amer. Math. Soc. 124 (11) (1996), 3293–3298.Google Scholar
Arens, R. F. and Kaplansky, I., ‘Topological representation of algebras’, Trans. Amer. Math. Soc. 63 (1948), 457–481.Google Scholar
Azumaya, G., ‘Strongly $\pi $-regular rings’, J. Fac. Sci. Hokkaido Univ. Ser. I 13 (1954), 34–39.Google Scholar
Bergman, G. M., ‘The diamond lemma for ring theory’, Adv. Math. 29 (2) (1978), 178–218.Google Scholar
Burgess, W. D. and Raphael, R., ‘On embedding rings in clean rings’, Comm. Algebra 41 (2013), 552–564.Google Scholar
Canfell, M. J., ‘Completion of diagrams by automorphisms and Bass’ first stable range condition’, J. Algebra 176 (2) (1995), 480–503.Google Scholar
Dischinger, F., ‘Sur les anneaux fortement $\pi $-réguliers’, C. R. Acad. Sci. Paris Sér. A–B 283 (8) (1976), Aii, A571–A573 (in French).Google Scholar
Hartwig, R. E. and Luh, J., ‘On finite regular rings’, Pacific J. Math. 69 (1) (1977), 73–95.CrossRefGoogle Scholar
Huang, L. S. and Xue, W., ‘An internal characterisation of strongly regular rings’, Bull. Aust. Math. Soc. 46 (3) (1992), 525–528.CrossRefGoogle Scholar
Kaplansky, I., ‘Topological representation of algebras. II’, Trans. Amer. Math. Soc. 68 (1950), 62–75.Google Scholar
Lam, T. Y., ‘Exercises in modules and rings’, in: Problem Books in Mathematics (Springer, New York, NY, 2007).Google Scholar
Nicholson, W. K., ‘Lifting idempotents and exchange rings’, Trans. Amer. Math. Soc. 229 (1977), 269–278.Google Scholar
Rangaswamy, K. M. and Vanaja, N., ‘A note on modules over regular rings’, Bull. Aust. Math. Soc. 4 (1971), 57–62.Google Scholar
Rowen, L. H., ‘Finitely presented modules over semiperfect rings’, Proc. Amer. Math. Soc. 97 (1) (1986), 1–7.Google Scholar
Yu, H.-P., ‘On strongly pi-regular rings of stable range one’, Bull. Aust. Math. Soc. 51 (3) (1995), 433–437.CrossRefGoogle Scholar