Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T17:58:27.705Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A PROBLEM OF RICHARD GUY

Part of: Diophantine equations

Published online by Cambridge University Press:  13 September 2021

NGUYEN XUAN THO Open the ORCID record for NGUYEN XUAN THO [Opens in a new window]
NGUYEN XUAN THO*
Affiliation:
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Vietnam
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the 1993 Western Number Theory Conference, Richard Guy proposed Problem 93:31, which asks for integers n representable by 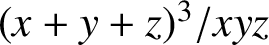${(x+y+z)^3}/{xyz}$ , where 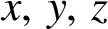$x,\,y,\,z$ are integers, preferably with positive integer solutions. We show that the representation 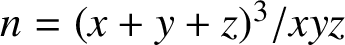$n={(x+y+z)^3}/{xyz}$ is impossible in positive integers 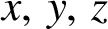$x,\,y,\,z$ if 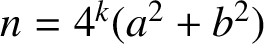$n=4^{k}(a^2+b^2)$ , where 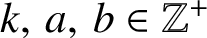$k,\,a,\,b\in \mathbb {Z}^{+}$ are such that 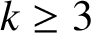$k\geq 3$ and 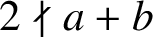$2\nmid a+b$ .

Keywords

cubic equationsp-adic numbersHilbert symbols

MSC classification

Primary: 11D25: Cubic and quartic equations
Secondary: 11D88: $p$-adic and power series fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 12 - 18
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 10.04-2019.314).

References

Bremner, A. and Guy, R. K., ‘Two more presentation problems’, Proc. Edinb. Math. Soc. 40(1) (1997), 1–17.CrossRefGoogle Scholar
Bremner, A. and Tho, N. X., ‘The equation $\left(w+x+y+z\right)\left(1/ w+1/ x+1/ y+1/ z\right)=n$ ’, Int. J. Number Theory 14(5) (2018), 1229–1246.CrossRefGoogle Scholar
Brueggeman, S. A., ‘Integers representable by ${\left(x+y+z\right)}^3/ xyz$ ’, Int. J. Math. Math. Sci . 21(1) (1998), 107–116.CrossRefGoogle Scholar
Dofs, E. and Tho, N. X., ‘On the Diophantine equation ${x}_1/ {x}_2+{x}_2/ {x}_3+{x}_3/ {x}_4+{x}_4/ {x}_1=n$ ’, Int. J. Number Theory, to appear, https://doi.org/10.1142/S1793042122500075.Google Scholar
Garaev, M. Z., ‘Third-degree Diophantine equations’, in Analytic Number Theory and Applications: Collection of papers to Prof. Anatolii Alexeevich Karatsuba on the occasion of his 60th birthday, Trudy MIAN 218 (1997), 99–108; English translation, Proc. Steklov Inst. Math. 218 (1997), 94–103.Google Scholar
Garaev, M. Z., ‘On the Diophantine equation ${\left(x+y+z\right)}^3= nxyz$ ’, Vestnik Moskov. Univ. Ser. I Mat. Mekh. 2 (2001), 66–67.Google Scholar
Guy, R. K., ‘Problem 93:31’, Western Number Theory Problems 93(12) (1993), 21.Google Scholar
Serre, J. P., A Course in Arithmetic, Graduate Texts in Mathematics, 7 (Springer, New York, 1973).CrossRefGoogle Scholar
Stoll, M., Answer to: ‘Estimating the size of solutions of a Diophantine equation’, https:// mathoverflow.net/questions/227713/estimating-the-size-of-solutions-of-a-diophantine-equation.Google Scholar
Tho, N. X., ‘On a Diophantine equation’, Vietnam J. Math., to appear, https://doi.org/10.1007/s10013-021-00503-w.Google Scholar
Tho, N. X., ‘What positive integers n can be presented in the form $n=\left(x+y+z\right) \left(1/ x+1/ y+1/ z\right)?$ ’, Ann. Math. Inform, to appear, https://doi.org/10.33039/ami.2021.04.005.Google Scholar