No CrossRef data available.
Published online by Cambridge University Press: 27 May 2019
This note provides an affirmative answer to Problem 2.6 of Praeger and Schneider [‘Group factorisations, uniform automorphisms, and permutation groups of simple diagonal type’, Israel J. Math. 228(2) (2018), 1001–1023]. We will build groups 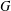 $G$ (abelian, nonabelian and simple) for which there are two automorphisms
$G$ (abelian, nonabelian and simple) for which there are two automorphisms 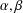 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$ of 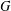 $G$ such that the map is surjective.
$G$ such that the map is surjective.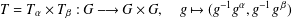 $$\begin{eqnarray}T=T_{\unicode[STIX]{x1D6FC}}\times T_{\unicode[STIX]{x1D6FD}}:G\longrightarrow G\times G,\quad g\mapsto (g^{-1}g^{\unicode[STIX]{x1D6FC}},g^{-1}g^{\,\unicode[STIX]{x1D6FD}})\end{eqnarray}$$
$$\begin{eqnarray}T=T_{\unicode[STIX]{x1D6FC}}\times T_{\unicode[STIX]{x1D6FD}}:G\longrightarrow G\times G,\quad g\mapsto (g^{-1}g^{\unicode[STIX]{x1D6FC}},g^{-1}g^{\,\unicode[STIX]{x1D6FD}})\end{eqnarray}$$