Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T14:58:45.287Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A PROBLEM OF CHEN AND LEV

Part of: Sequences and sets

Published online by Cambridge University Press:  28 November 2018

SHI-QIANG CHEN ,
MIN TANG  and
QUAN-HUI YANG
SHI-QIANG CHEN
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, PR China email [email protected]
MIN TANG*
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, PR China email [email protected]
QUAN-HUI YANG
Affiliation:
School of Mathematics and Statistics, Nanjing University of Information, Science and Technology, Nanjing 210044, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

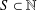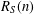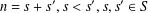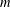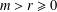For a given set $S\subset \mathbb{N}$, $R_{S}(n)$ is the number of solutions of the equation $n=s+s^{\prime },s<s^{\prime },s,s^{\prime }\in S$. Suppose that $m$ and $r$ are integers with $m>r\geq 0$ and that 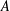$A$ and 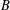$B$ are sets with 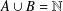$A\cup B=\mathbb{N}$ and 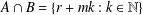$A\cap B=\{r+mk:k\in \mathbb{N}\}$. We prove that if 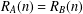$R_{A}(n)=R_{B}(n)$ for all positive integers $n$, then there exists an integer 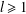$l\geq 1$ such that 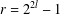$r=2^{2l}-1$ and 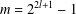$m=2^{2l+1}-1$. This solves a problem of Chen and Lev [‘Integer sets with identical representation functions’, Integers16 (2016), A36] under the condition 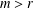$m>r$.

Keywords

partitionrepresentation functioncharacteristic function

MSC classification

Primary: 11B34: Representation functions
Secondary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 15 - 22
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author was supported by the National Natural Science Foundation of China, Grant No. 11471017. The third author was supported by the National Natural Science Foundation for Youth of China, Grant No. 11501299, the Natural Science Foundation of Jiangsu Province, Grant Nos. BK20150889 and 15KJB110014, and the Startup Foundation for Introducing Talent of NUIST, Grant No. 2014r029.

References

Chen, Y. G. and Lev, V. F., ‘Integer sets with identical representation functions’, Integers 16 (2016), A36, 4 pages.Google Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.Google Scholar
Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, I’, Pacific J. Math. 118 (1985), 347–357.Google Scholar
Erdős, P. and Sárközy, A., ‘Problems and results on additive properties of general sequences, II’, Acta Math. Hungar. 48 (1986), 201–211.Google Scholar
Erdős, P., Sárközy, A. and Sós, V. T., ‘Problems and results on additive properties of general sequences, III’, Studia Sci. Math. Hungar. 22 (1987), 53–63.Google Scholar
Erdős, P., Sárközy, A. and Sós, V. T., ‘Problems and results on additive properties of general sequences, IV’, in: Number Theory, Proceedings, Ootacamund, India, 1984, Lecture Notes in Mathematics, 1122 (Springer, Berlin, 1985), 85–104.Google Scholar
Erdős, P., Sárközy, A. and Sós, V. T., ‘Problems and results on additive properties of general sequences, V’, Monatsh. Math. 102 (1986), 183–197.Google Scholar
Kiss, S. Z. and Sándor, C., ‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161.Google Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electron. J. Combin. 11 (2004), R78, 6 pages.Google Scholar
Li, J. W. and Tang, M., ‘Partitions of the set of nonnegative integers with the same representation functions’, Bull. Aust. Math. Soc. 97 (2018), 200–206.Google Scholar
Rozgonyi, E. and Sándor, C., ‘An extension of Nathanson’s theorem on representation functions’, Combinatorica 37 (2016), 1–17.Google Scholar
Sándor, C., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), A18, 5 pages.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.Google Scholar
Tang, M., ‘Partitions of natural numbers and their representation functions’, Chinese Ann. Math. Ser A 37 (2016), 41–46; English translation, Chinese J. Contemp. Math. 37 (2016), 39–44.Google Scholar
Yu, W. and Tang, M., ‘A note on partitions of natural numbers and their representation functions’, Integers 12 (2012), A53, 5 pages.Google Scholar