No CrossRef data available.
Published online by Cambridge University Press: 08 February 2022
For a set A of positive integers and any positive integer n, let
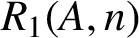 $R_{1}(A, n)$
,
$R_{1}(A, n)$
,
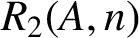 $R_{2}(A,n)$
and
$R_{2}(A,n)$
and
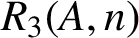 $R_{3}(A,n)$
denote the number of solutions of
$R_{3}(A,n)$
denote the number of solutions of
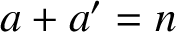 $a+a^{\prime }=n$
with
$a+a^{\prime }=n$
with
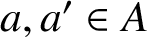 $a, a^{\prime }\in A$
and the additional restriction that
$a, a^{\prime }\in A$
and the additional restriction that
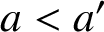 $a<a^{\prime }$
for
$a<a^{\prime }$
for
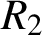 $R_{2}$
and
$R_{2}$
and
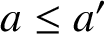 $a\leq a^{\prime }$
for
$a\leq a^{\prime }$
for
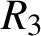 $R_{3}$
. We consider Problem 6 of Erdős et al. [‘On additive properties of general sequences’, Discrete Math. 136 (1994), 75–99] about locally small and locally large values of
$R_{3}$
. We consider Problem 6 of Erdős et al. [‘On additive properties of general sequences’, Discrete Math. 136 (1994), 75–99] about locally small and locally large values of
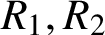 $R_{1}, R_{2}$
and
$R_{1}, R_{2}$
and
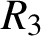 $R_{3}$
.
$R_{3}$
.
This work was supported by the National Natural Science Foundation of China (Grant No. 11971033) and top talents project of Anhui Department of Education (Grant No. gxbjZD05).